Hello All!
As an engineer I am skeptic. I think without validation no FE results should be accepted. That is why I tested SimScale with one of my favourite steady state thermal benchmarks. The example is as described in the followings:
We have a steel rod with 1 m length (H=1 m), with a cylindrical cross section (d=0.1 m). The one end of the rod is hot (t0=100°C), while the other surfaces of the body are surrounded by air which hase a temperature of 20°C (this is t infinite). See the picture below.
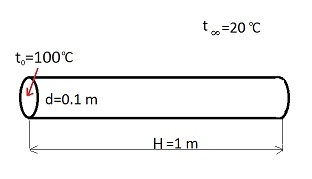
We assume that the thermal conductivity of the rod (lambda) is 73 W/mK and the convection in the air (alpha) has a value of 40 W/m2K. Further on we assume that the material of the rod is homogeneous and its cross section is constant. Under these conditions if we neglect the heat convection at the free end of the rod the temperature distribution of the body can be described in a very simple form in steady state:
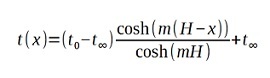
where “m” is expressed as follows:
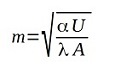
where “U” is the perimeter of the cross section and “A” is the area of it while “x” is the moving coordinate along the legth “H”.
I built up the upper model in SimScale. Just follow the link: https://www.simscale.com/workbench?publiclink=0e6b87dd-d4c5-4091-8e93-dd6d005df569
However it was not easy to get the nodal results, but thanks to the unbelievable help of ahmedhussain18 and ggiraldo I succeded it using the ParaView software which is an open source post processor. The method to get nodal results see under the following link: How to get nodal solution results?
And finally I compared the analytical results with the FE simulation ones and on the diagram below you can see the perfect match of both:
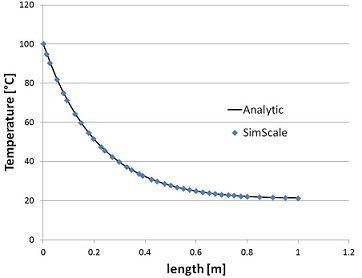
The diagram shows the temperature distribution along the length of the rod in steady state over the length of the rod. The analytical result is depicted by a continous black line, while the SimScale results are symbolized by blue dots.
I think the reliability of the solver is proven for this type of problems.
And finally you can see below a result picture in the post processor of SimScale: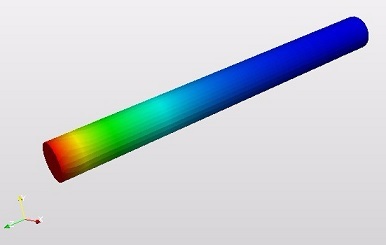
and in ParaView:
\underline{\textbf{Visit our SimWiki by clicking on the picture}}
to 