Convergence checking

jkaka · November 30, 2021, 6:50am

Hi please can i say that the result is convergent?

jkaka · November 30, 2021, 1:25pm

please can someone help me ???

ggiraldof · November 30, 2021, 1:57pm

Hey there!

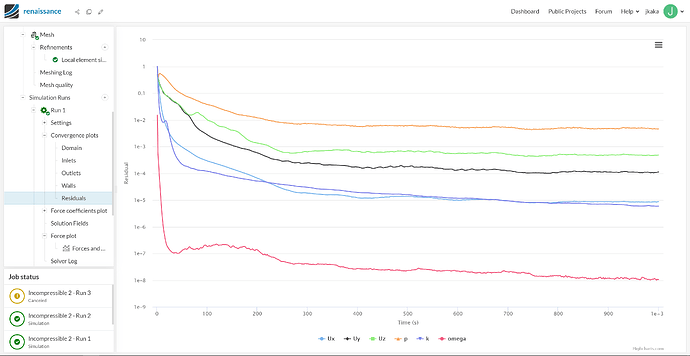
This plot, which is the convergence of the residuals, shows the maximum residual over the whole domain. If it is low enough, say all curves below 0.001, then we can say that the computation is most likely converged. But sometimes, there might be regions, often close to the boundaries, where the residuals are high while in other regions the residuals are low. This can mess with the plot you show.

To really tell if the computation is converged, you should be rather looking at the Force plot. As this is your variable of interest, you want this to be converged, and the residuals are mostly secondary.

jkaka · November 30, 2021, 2:05pm

thanks sir but this is not converge right?

ggiraldof · November 30, 2021, 3:03pm

I would say that it is mostly converged. You can tell for example by zooming in to the last 100 iterations, and checking the ratio of the amplitude of the variations to the mean value. If it is small, say 5%, then you can tell it is converged.

If you want to improve such ratio, then you have to perform a mesh independence analysis, e.g. refine the mesh around the area of interest.

jkaka · November 30, 2021, 8:04pm

ok thank you sir

jairogut · December 1, 2021, 3:48pm

Yeah, @ggiraldof is right. I will only add that the result is as converged as your grid allows for. You are using a very coarse grid. I suggest you learn to use hex-dominant parametric and do gradual refinements. Those, especially in the trailing edge, are crucial for the accuracy of the calculations. Refine where flow separation or large gradients are expected.

jkaka · December 2, 2021, 5:20am

ok, thank you sir

DaleKramer · November 5, 2023, 1:37pm

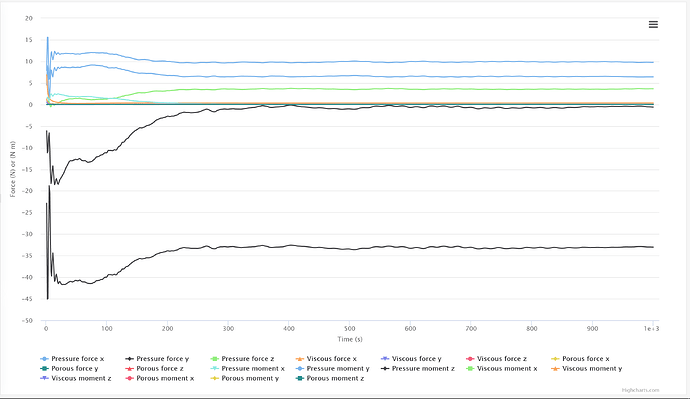
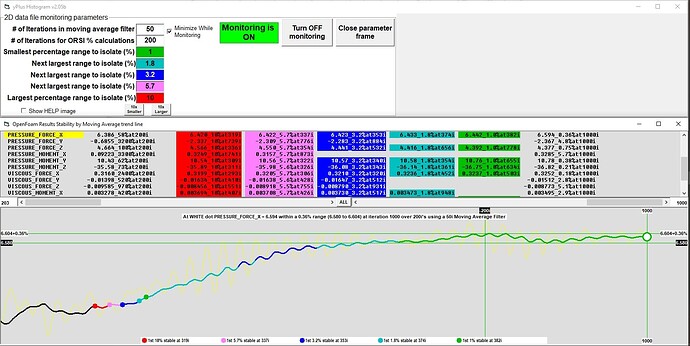
I know this topic is solved but I wanted to test my recent upgrade to v205b of my yPlusHistogram programs’ ORSI feature on the force convergence shown in Post 4.

Here is SimScale representation of all the ‘Forces’ parameter convergence (this was also shown in Post 4):

Here is the same data using the ORSI plotter graphing the selected yellow PRESSURE_FORCE_X results (in ORSI interface you can select all the other Force parameters but only 1 parameter can be plotted at once):

I would conclude that most of the Force parameters are extremely stable and ORSI allows a way to numerically quantify the stability of all the parameters individually.