Hi all,
As much as it is going to sound like a feature request, it is not. I am bringing it up because I have followed SimScale for a while and haven’t noticed any trace that these following features are enabled. Your team may be already working on some of them.
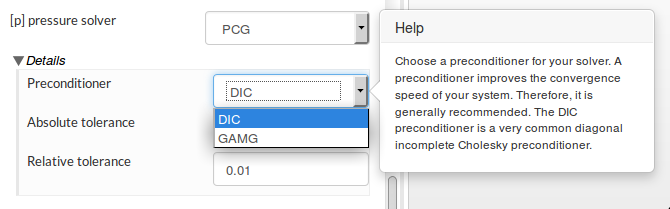
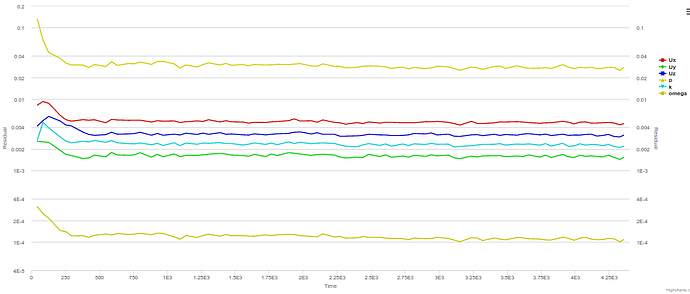
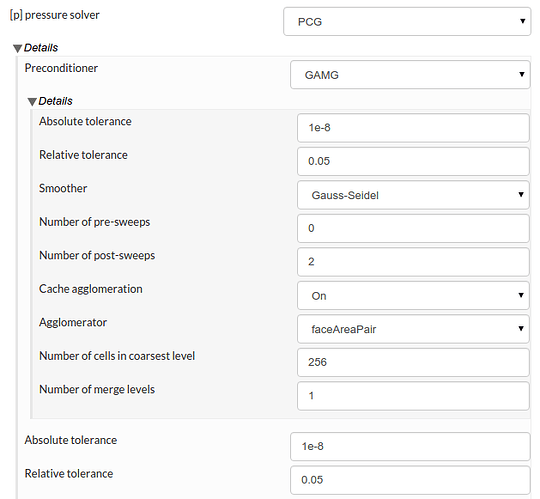
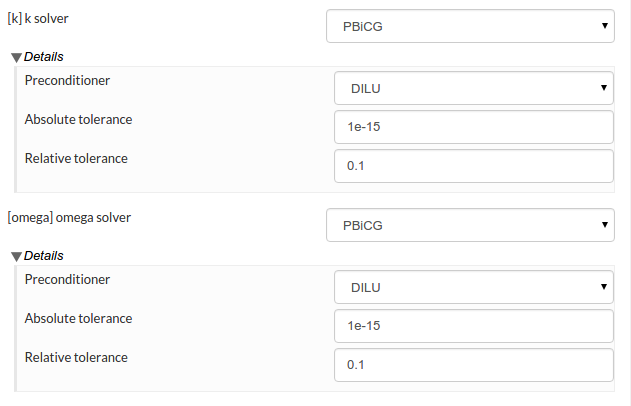
Firstly, I would like to ask what is the Krylov subspace method preconditioned by? From David’s recent reply to the GT350R simulation, it doesn’t look like it is preconditioned by multi-grid. There have been quite a few studies including my own testing that concluded multi-grid preconditioned (Bi) Conjugate gradient is faster than multi-grid by itself. While AMG results in a much faster convergence, Krylov subspace methods scale better in parallel computation.
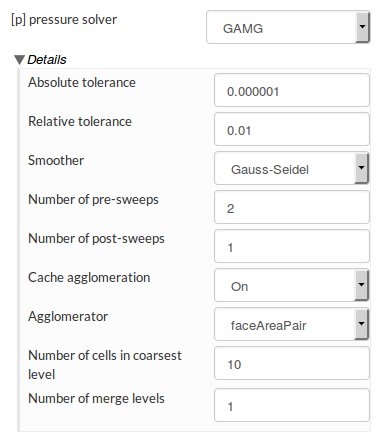
Secondly, I have noticed within AMG, one is not allowed to customise the solver. Things such as the number of pre/post sweeps and v-cycles ( 2 by default ), merge levels, smoother etc. In some case, speedup is significant by altering those parameters, specially when going with ILU a higher merge level can be used.
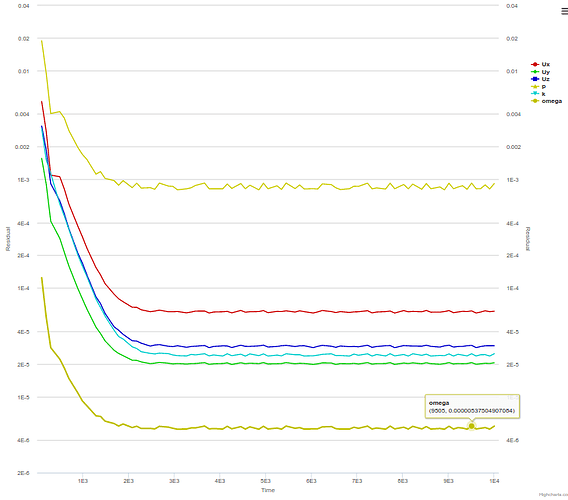
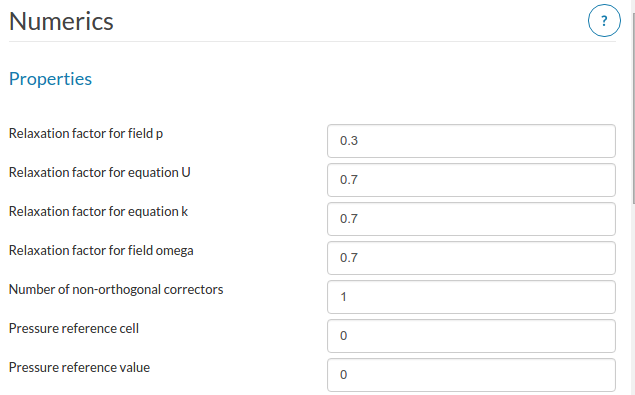
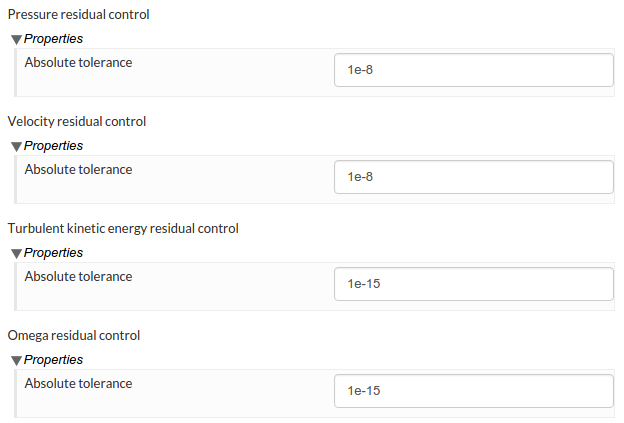
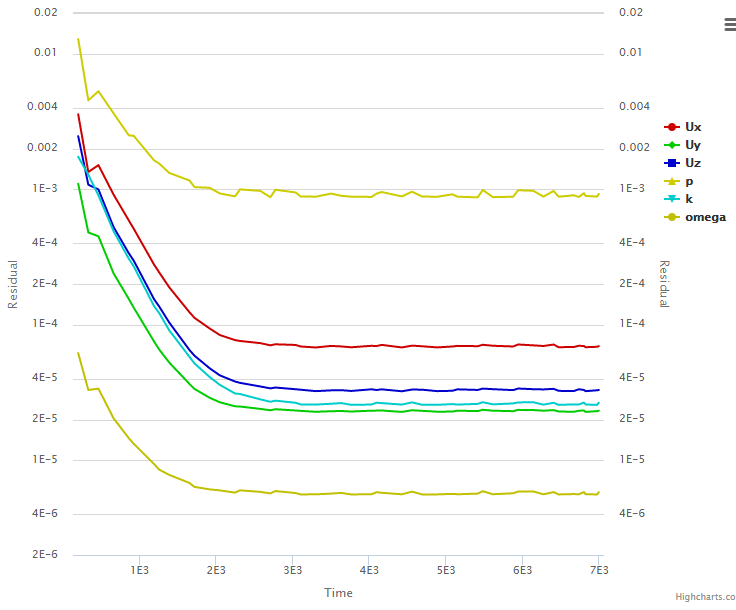
Thirdly, there doesn’t seem to be a relative tolerance control for steady state computation. It is very useful to use a large relative tolerance in steady state, because in this case it is the initial residuals at the start of each SIMPLE loop (time step) that matter, rather than the final residuals at the end of those loops. With a large relative tolerance, the solve will then quickly move onto a newer SIMPLE loop and therefore the initial residuals will drop more ( with more iterations ). The same outcome can be achieved by limiting max number of iterations within each loop.
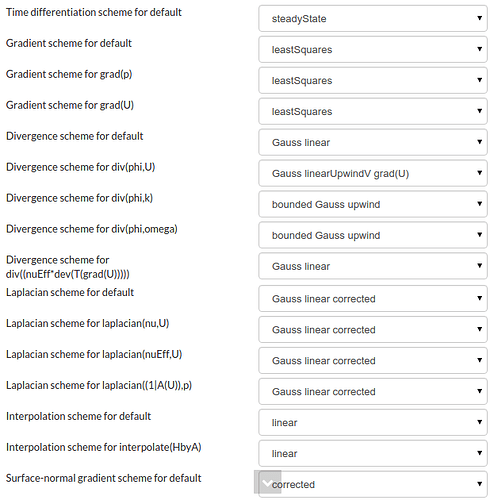
The second last point I would like to bring up is about the schemes available. Although there are a variety of discretisation schemes for convective terms, none of them seem adequate for scale-resolving computations. The limitedLinear is a central differencing with the Sweby limiter. This TVD scheme is less dissipative than linearUpwind but is, I believe, still far too dissipative for LES. The scheme I usually use for convective terms is LUST, while Gamma can be useful in a few cases. A pure central differencing can be too expensive to afford.
Finally, the SIMPLEC algorithm is significantly faster than SIMPLE when the flow field has a weak coupling in physics, as no pressure underrelaxation is required and larger underrelaxation factors can be used on the other fields ( velocities and turbulence parameters ). Examples of such flows are isothermal incompressible and mildly compressible flows. I have pretty much only used SIMPLC to compute external incompressible/compressible aerodynamics in steady state.
Looking forward to all of your replies.