What Happens If a Power Source Partially Intersects with a Domain?

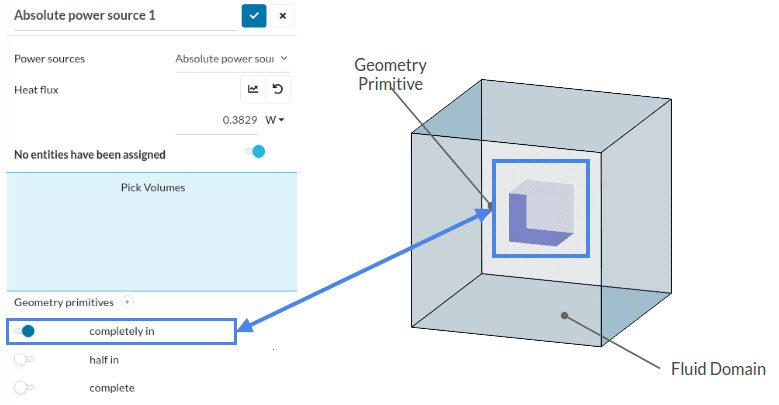
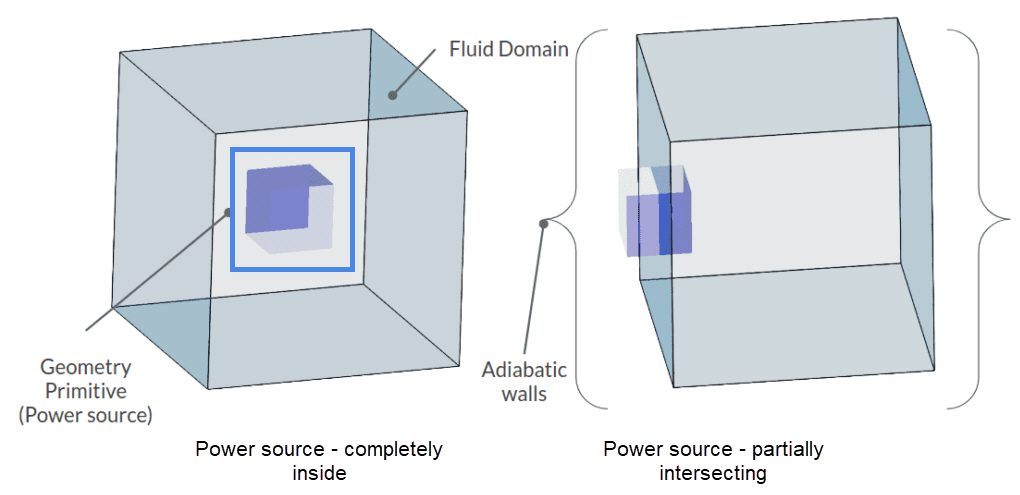
This article discusses a situation where a power source only partially intersects with a domain, rather than completely taking up space inside the domain.

Power sources can be assigned to a part in the CAD model or to a geometry primitive. If an absolute power source is assigned to the geometry, this means absolute power will be dissipated from the volume of the selected entity. In other words, heat generation from every cell within the selected entity will be:

$$ Power_{cell} = \frac{Absolute \, Power}{Number \, of \, Cells} $$

If the entity is not completely intersecting with the domain, the domain cannot receive full power. This is explained in the following example:

Example – Heat Source Inside a Fluid Domain

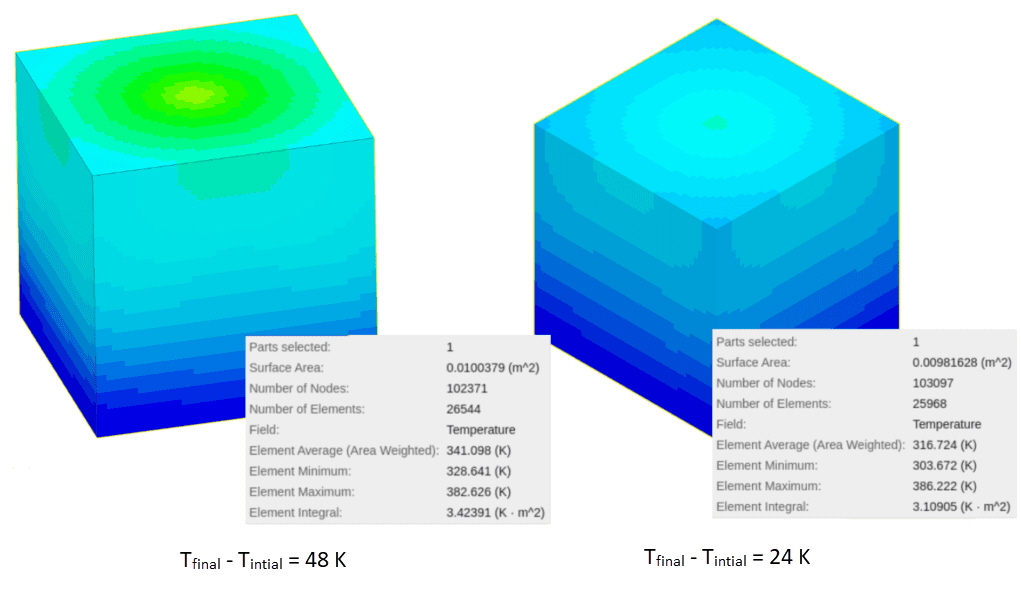
In this example, we are testing two setups. In the first setup, a cartesian box geometry primitive is completely inside the fluid domain. In the second one, only half of it lies inside. In each setup, walls of the fluid domain are adiabatic and 0.38288 \(W\) of absolute power is assigned to the geometry primitives. The simulation type is transient conjugate heat transfer. The initial temperature for both cases is 293 \(K\) and the simulation takes place for 10 seconds.

As stated before, power is dissipated as volumetric heat flux. Therefore, the second domain will only receive half of the absolute power, which is generated by the geometry primitive. Based on energy balance, one should expect the temperature change in the second set up to be half of the first one:

$$ P = m . C_p . \Delta T $$

Where, \(P\) is the power \([W \cdot s]\), \(m\) is the mass of the fluid volume \([kg]\). \(C_p\) is the specific heat capacity of the fluid \([J/kgK]\), and \(\Delta T \) is the difference between initial and final average fluid temperature. The results of the stated example validate the theory.