Error: Matrix is Singular / Not Factorizable

What Happened?

The solution couldn’t proceed since the matrix is singular (not factorable matrix).

What Could Be the Possible Reason?

This error may occur due to several reasons, which are:

• Poorly defined boundary conditions. An uninvertible matrix can be caused by poorly defined constraints. For example, applying only a load without constraining the geometry.
• Some nodes are overconstrained, due to multiple constraints assigned in the same direction from different boundary conditions, contacts, physical contacts, or a combination of those.
• Units of material properties such as Young’s modulus are not consistent with the dimensions of the geometry.
• A body is only constrained by its contact with another solid body when using linear sliding contacts or nonlinear physical contacts. This causes the body to move freely in all directions which causes the matrix to become uninvertible.
• Duplicated contact assignment on the same pair of faces, with reversed order of master/slave.
• Node belongs to multiple contact slave assignments.
• Using Multfront or LDLT for non-positive-definite matrices (negative or zero eigenvalues) under Numerics.
• Use of smaller value for Precision singularity detection under Numerics.

What Can I Do Now?

Do the following steps to resolve this error:

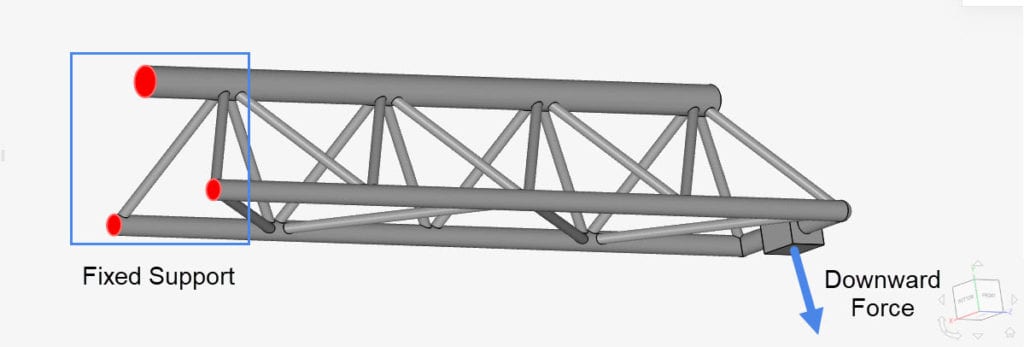
• Evaluate the boundary conditions: Make sure that your geometry is properly constrained. For example, in the crane tutorial, the crane is fixed on one end while receiving a downward force on the other end and no faces are constrained with multiple boundary conditions. Also, make sure that the nodes are not overconstrained. This might happen due to improper boundary conditions on adjacent faces sharing nodes/edges.

• Check if the material parameters provided are consistent with the geometry dimensions or not: For structural analysis, units of physical and material parameters must be consistent with each other. The units for each parameter based on its standards can be seen below:

Parameter	SI	SI	Imperial
Length	\(m\)	\(mm\)	\(in\)
Force	\(N\)	\(N\)	\(lbf\)
Stress / Young’s Modulus	\(Pa\ (N/m^2)\)	\(MPa\ (N/mm^2)\)	\(psi\ (lbf/in^2)\)
Density	\(kg/m^3\)	\(kg/mm^3\)	\(lb/in^3\)

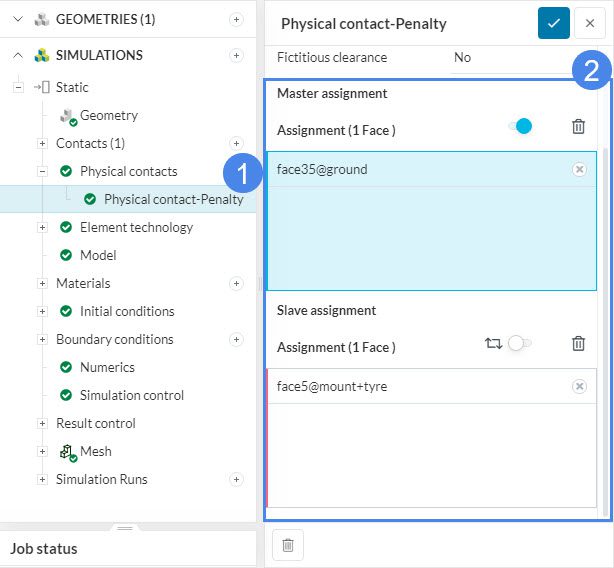
• Evaluate physical contact definitions: Two contacts should not be defined on the same pair surfaces with reverse order of master/slave assignments. One contact is enough to fulfill the requirement. Consider running automatic contact detection again. Also, multiple slave surfaces from different contact definitions should not share nodes. One has to be the master surface among these surfaces. As an example, please see the Shared slave nodes error case. You can check this in your Physical contacts settings.

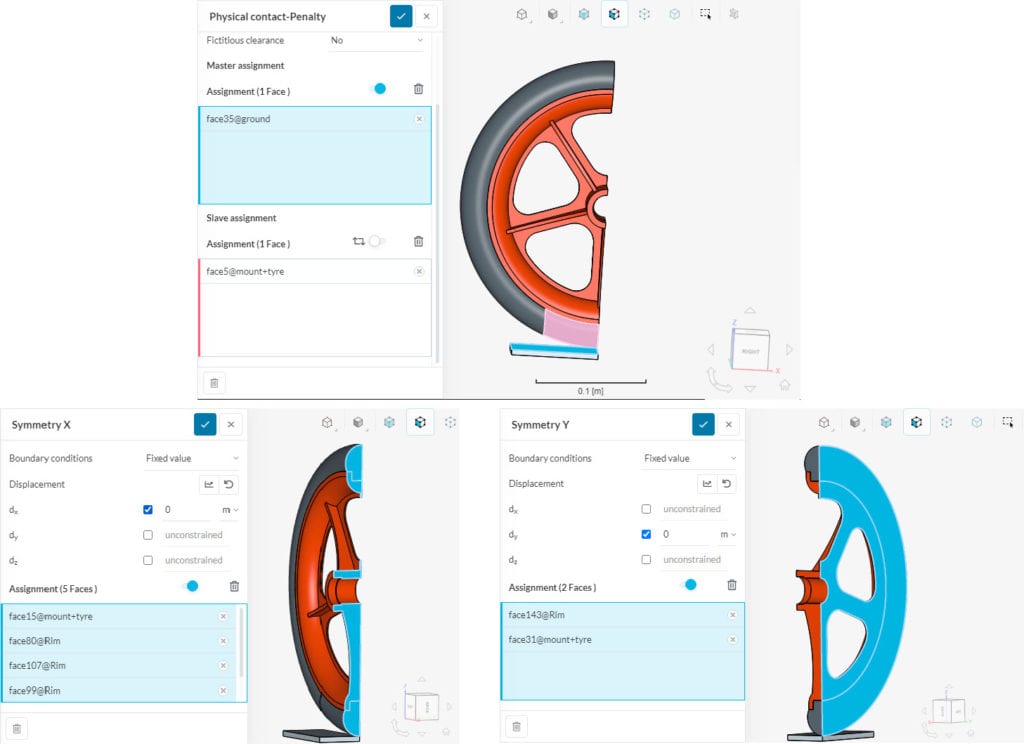
• Find unconstrained body when using linear sliding contacts or non-linear physical contacts: Constrain the free structure so that it is held by the constrained boundary condition and by the contact. For example, the wheel below is constrained by the physical contact with the ground and the x- and y-plane to constrain the movement in each plane.

• Bodies with sliding or nonlinear physical contact should not be constrained in such a way that they can’t deform. This happens when a fixed constraint or rotating motion is applied to the whole volume.
• Use the ‘MUMPS’ solver: In the case of zero or negative eigenvalues, make sure that you are using ‘MUMPS’ which can handle non-positive-definite matrices better than ‘Multfront’ and ‘LDLT’. These settings can be changed in Numerics.

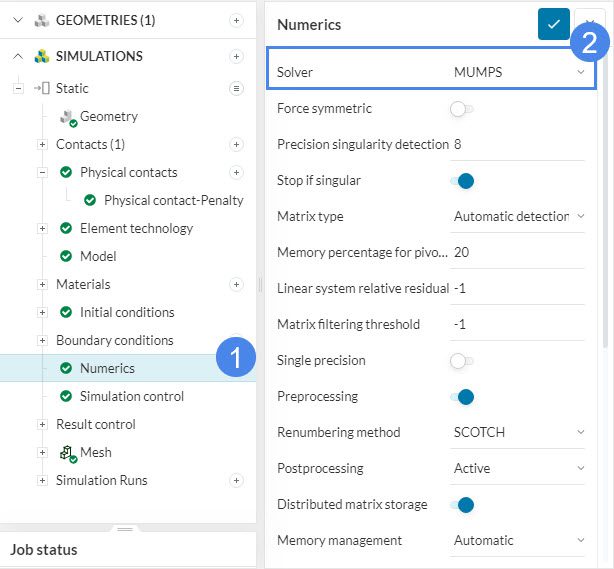
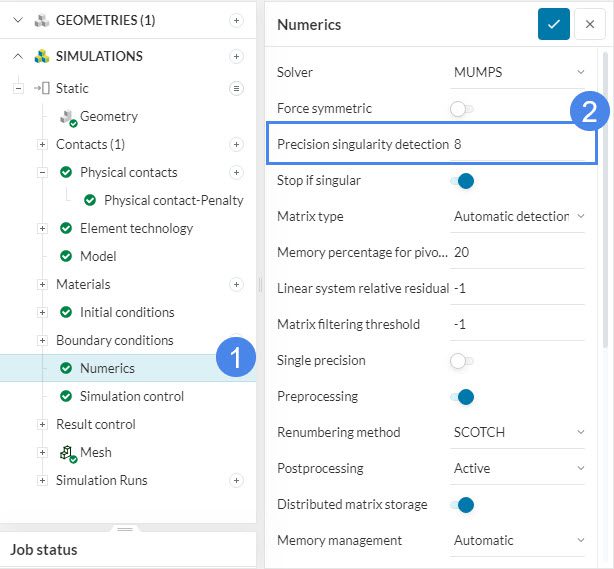
• Increase the value of ‘Precision singularity detection’: This will allow the solver to continue despite imprecise detection of singularity. This setting can also be found under Numerics.