websights

Fill out the form to download

Required field
Required field
Not a valid email address
Required field
Required field

  • Set up your own cloud-native simulation in minutes.

    • Documentation

    SimScale DocumentationKnowledge BaseHow to Model the Ground Roughness in Incompressible Analysis?

    How to Model the Ground Roughness in Incompressible Analysis?

    Created On
    byMehmet Oezcan

    This article explains the best practices for modelling the ground roughness in SimScale’s incompressible flow simulation, which can also be applied to other simulations. For example, a convective heat transfer or conjugate heat transfer analysis.

    One of the most influencing factors in an external aerodynamic simulation is ground roughness, therefore it is can be important to model the ground roughness in a CFD simulation.

    vertical velocity profile visualized with comets
    Figure 1: Vertical velocity profile

    Important

    The concepts and workflow below can be applied to the fluid dynamic solvers based on OpenFOAM®.

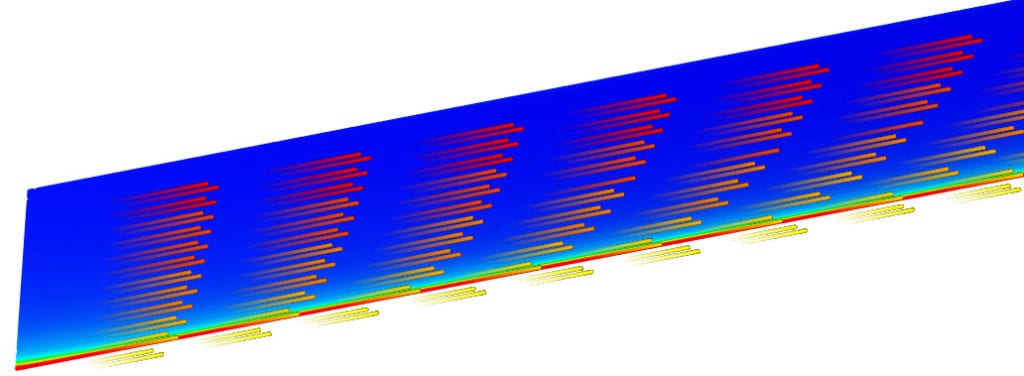
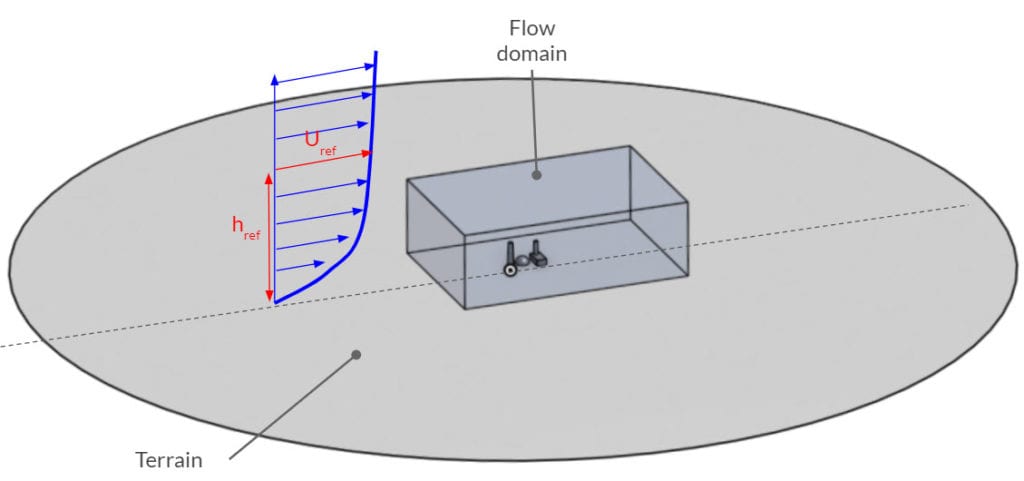
    A Fully Developed ABL Profile

    Atmospheric Boundary Layer (ABL) is a model to explain the earth’s lower atmosphere and its behaviour with respect to the ground. On the other hand, the velocity (\(u\)) profile is assumed to be logarithmic and turbulent kinetic energy (\(k\)) and turbulent dissipation rate \(\varepsilon\) are height dependent.

    figure showing the relationship between velocity profile, flow domain and terrain
    Figure 2: Relationship between flow domain, velocity profile and terrain

    Moreover, if you need more information regarding how to calculate ABL profile, please visit this knowledge base article.

    Sand-Grain Roughness Modification

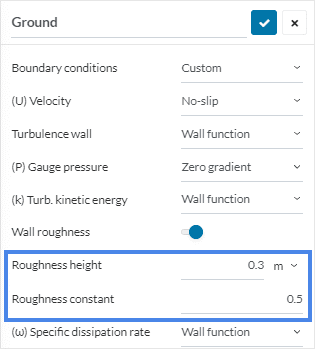
    The incompressible flow simulation solver implemented in SimScale uses wall functions as default. Hence, the rough wall function model uses equivalent sand-grain roughness (\(k_s\)) and roughness constant (\(C_s\)) parameters.

    This wall function is originally developed for pipe flows, therefore the aerodynamic roughness length (\(z_0\)) should be modified for equivalent roughness. Likewise, a good approximation for an equivalent sand-grain roughness takes both the terrain aerodynamic roughness length and a roughness constant into account which can be expressed with the equation below:

    $$k_s = \frac{9.793 \cdot z_0}{C_s} \tag{1}$$

    setup parameters for assigning roughness height and roughness constant
    Figure 3: Assignment of roughness height and roughness constant

    In the following table, you will see the mean terrain roughness length (\(z_0\)) per terrain class, and corresponding roughness length (\(k_s\)) and minimum first cell height requirements in CFD modeling. Cell size values are calculated for roughness constant of 1 (\(C_s\)), but you can multiply the height by 2 if you need to use roughness constant of 0.5. [1]

    Terrain Classmean \(z_0\) [m]\(k_s\) [m]\(C_s\)h [m]
    10.00010.00110.002
    20.00050.004910.01
    30.0050.04910.1
    40.030.293810.6
    50.070.685511.4
    60.555.3862110.8
    72.524.4825149
    Table 1: Surface roughness based on terrain class

    Basic Recommendations for an Accurate ABL Profile

    However, an accurate representation of ABL profile on the near ground regions may be challenging to achieve in CFD, therefore there are many studies on how to achieve the most accurate results. For example, a study from Blocken et al. [2] suggested the following measures to capture the ABL profile as close as possible:

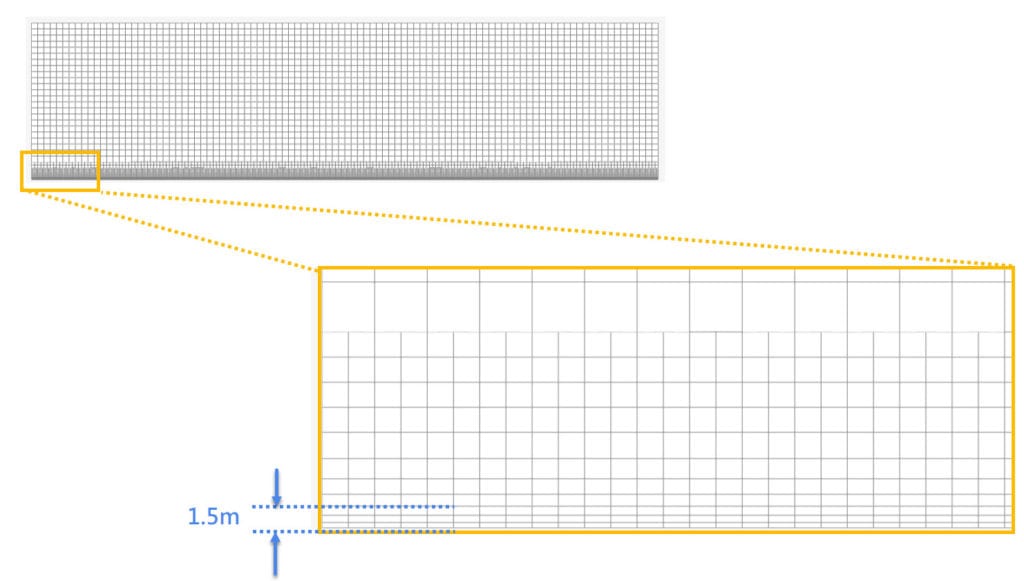
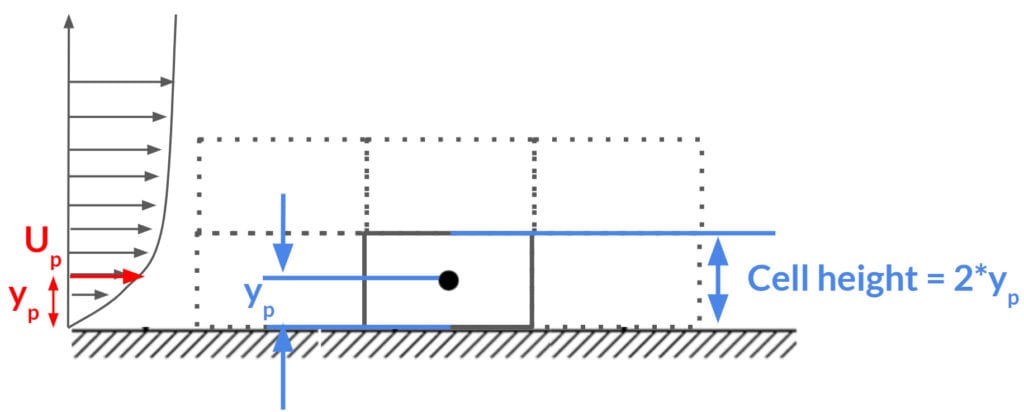
    1. Firstly, You need a high mesh resolution around the ground level. A minimum of 2 or 3 elements (or layers) is required for pedestrian wind comfort simulations. In general, keep the first cell height less than 1 \(m\).
    example of mesh with refinements at the pedestrian level and the height of the first 3 cells is 1.5 m
    Figure 4: Horizontal flow domain meshing strategy

    2. Keep the height of the center point \(y_p\) of the first cell (or layer) larger than the equivalent sand grain roughness height \(k_s\) (\(y_p\)>\(k_s\)).

    figure showing the mesh requirement in relatonship with sand grain roughness height
    Figure 5: Height of first cell in relation to height of sand grain roughness

    3. Lastly, make sure that the ABL profile is homogeneous from the upstream to the downstream.

    homogenous velocity profile with sand grain roughness implemented
    Figure 6: Vertical velocity profile

    4. And then you can find a good approximation regarding the relationship between the \(k_s\) and \(z_0\).

    vertical velocity profile showing a stable atmospheric boundary layer
    Figure 7: Vertical velocity profile

    References

    • Toparlar, Y., Blocken, B., & Van Heijst, G.(2019). “CFD Simulation of the Near-neutral Atmospheric Boundary Layer: New Temperature Inlet Profile Consistent with Wall Functions”. Journal of Wind Engineering and Industrial Aerodynamics, 191, 91-102.https://doi.org/10.1016/j.jweia.2019.05.016
    • Blocken, B., Stathopoulos, T., & Carmeliet, J. (2007). “CFD simulation of the Atmospheric Boundary Layer: Wall Function Problems”. Atmospheric Environment, 41(2), 238-52.https://doi.org/10.1016/j.atmosenv.2006.08.019

    Note

    If none of the above suggestions solved your problem, then please post the issue on our forum or contact us.

    Tags:

    Last updated: July 13th, 2022

    Contents