Dale,
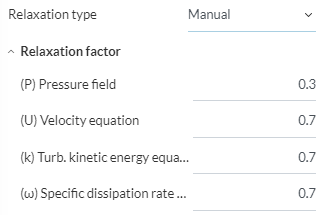
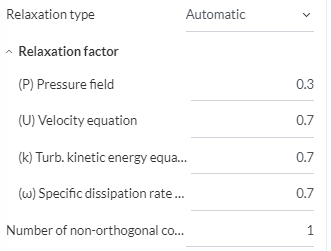
I am too struggling with some of these parameters, with much less knowledge then you or most of the other users on the forum. Currently, when manual is selected, these are the default settings.
And these are the settings for Automatic
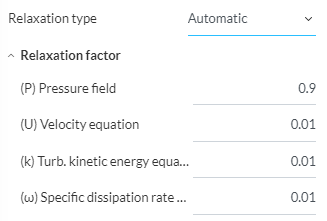
The automatic factors seem quite low (except for pressure) but i think someone on the forum told me that the automatic factors start out much higher, and are then tightened towards the end of the simulations. I just cant remember where that was said.
HOWEVER,
When doing some research on Non-Orthogonality, i did a small and basic thread here, with how mesh settings effects Non-orthogonal cell count.
For the simulation side, I found that using Non-Orthogonal corrector loops is necessary when there are higher numbers of Non-orthogonal cells, and when these cells have a higher angle (above 70 deg) Im not sure how strong the connection is between the corrector loops and relaxation factors, but my assumption is that both are necessary for convergence, especially with meshes of higher numbers of illegal cells.
Basically, as i understand it, most CFD solvers use the Over-relaxation method developed by Hrvoje Jasak, where the treatment of the explicit term during discretization allows for less corrector loops to achieve convergence. This is best said from his thesis:
Source:
Google Search
(Error Analysis and Estimation for the Finite Volume Method with Applications to Fluid Flows by: Hrvoje Jasak)
PG 113
In this study, the diffusion term will therefore be split into the implicit orthogonal contribution, which includes only the first neighbours of the cell and creates a diagonally equal matrix and the non orthogonal correction, which will be added to the source. If it is important to resolve the non-orthogonal parts of the diffusion operators (like in the case of the pressure equation, see Section 3.8), non-orthogonal correctors are included. The system of algebraic equations, Eqn. (3.42), will be solved several times. Each new solution will be used to update the non-orthogonal correction terms, until the desired tolerance is met. It should again be noted that this practice only improves the quality of the matrix but does not guarantee boundedness. If boundedness is essential, the non-orthogonal contribution should be discarded, thus creating a discretisation error described in Section 3.6.
Jasak is saying that if boundness (convergence) cannot be achieved, that the explicit term should be discarded. He then continues to say:
PG 114
The above discussion concentrates on the analysis of the discretisation on a term by-term basis. In reality, all of the above coefficients contribute to the matrix, thus influencing the properties of the system. It has been shown that the only terms that actually enhance the diagonal dominance are the linear part of the source and the temporal derivative. In steady-state calculations, the beneficial influence of the temporal derivative on the diagonal dominance does not exist. In order to enable the use iterative solvers, the diagonal dominance needs to be enhanced in some other way, namely through under-relaxation.
Then some confusing equations … followed by
PG 115
Here, (theta p) here represents the value of (theta)’ from the previous iteration and a is the under-relaxation factor (0 < a ^ 1).
And finally the relaxation factor definition from OpenFOAM
Source: OpenFoam
Under-relaxation works by limiting the amount which a variable changes from one iteration to the next, either by modifying the solution matrix and source prior to solving for a field or by modifying the field directly. An under-relaxation factor
specifies the amount of under-relaxation, ranging from none at all for
and increasing in strength as
. The limiting case where
represents a solution which does not change at all with successive iterations. An optimum choice of
is one that is small enough to ensure stable computation but large enough to move the iterative process forward quickly; values of
So as i understand it. Non-orthogonal corrector loops help to achieve accuracy. When the non-orthogonal component (explicit term) is too large, it must be discarded, leaving only the orthogonal contribution (implicit term). This leads to necessity of under relaxation factors to make up for the deletion of this non-orthogonal component in order to either get an accurate reading (lower relaxation factor values eg: 0.2, 05) or to allow the inaccuracies to slide, in favor of convergence and speed.
I am taking this assumption from the only source i have read on this topic, the thesis from Jasak. Please correct me, as i am only attempting to understand what is going on here and apply it to my simulations.
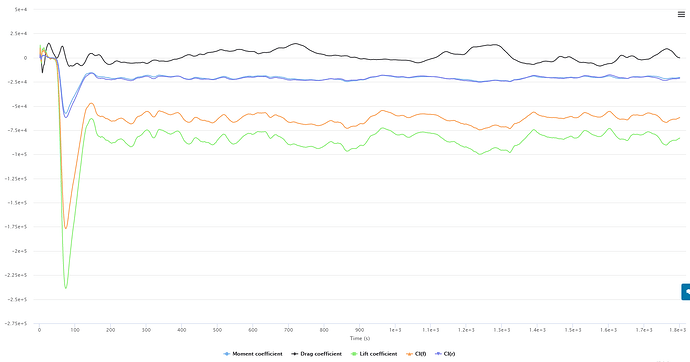
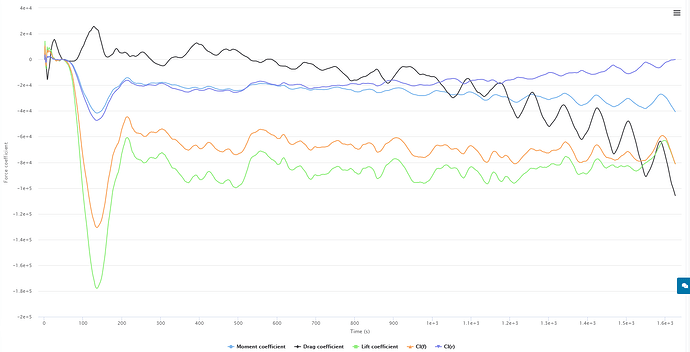
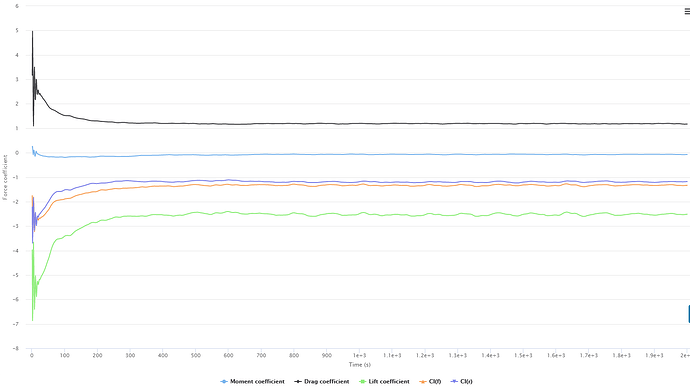
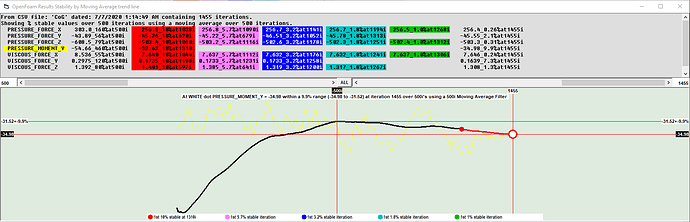
Working off of this information, I am currently getting some very incorrect numbers on my full car sims as shown below. Not to try and change the topic of discussion but i have changed both of these settings in hopes that they would help.
First run here shows the following coefficient graph that is very wrong.
Relaxation type: Automatic
Relaxation factors:
P = 0.3
U = 0.7
K = 0.7
W = 0.7
Non- orthogonal correction = 0
EDIT
Sim time = 21.76 hrs
Core hours = 695.5
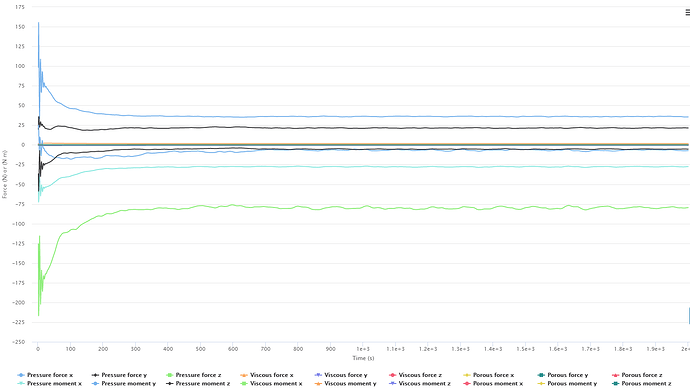
Second run: here reduced relaxation factors and added a non-orthogonal correction loop.
Relaxation type: Automatic
Relaxation factors:
P = 0.3
U = 0.7
K = 0.5
W = 0.5
Non- orthogonal correction = 1
EDIT
Sim time = 23.23 hrs
Core hours = 743.5
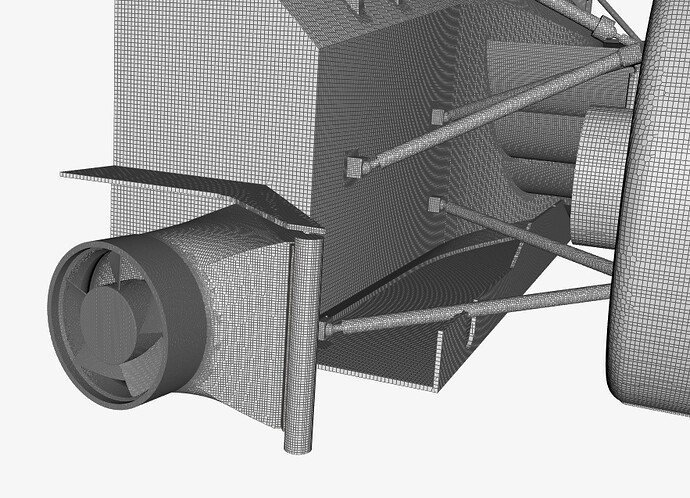
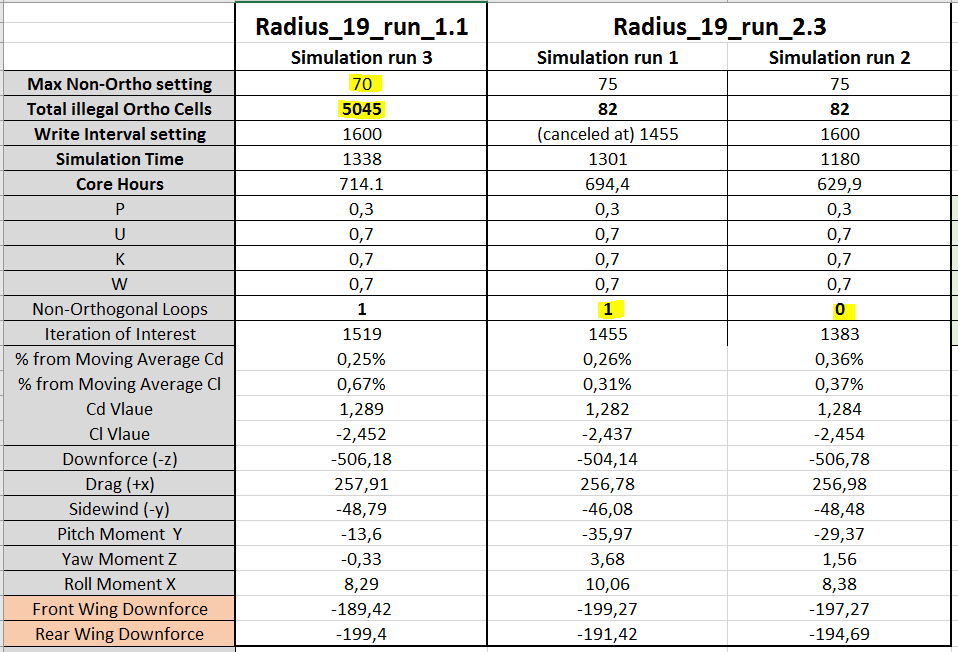
This brings me to the mesh quality as the most likely cause - here
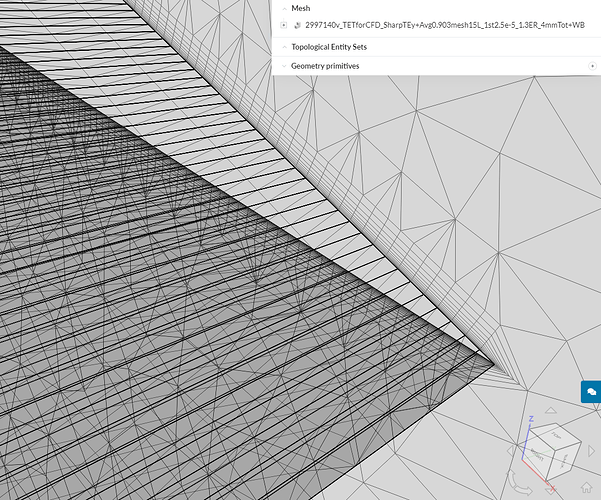
Most of my previous simulations done with Simscale have had a illegal cell count of around 2-500 with a 15-20 million total cell count. Most of the illegal cells are Non-orthogonal. These previous simulations also had the max non-orthogonal quality setting at 75 deg. When changing this value to 70 deg, the amount of non-orthogonal cells jumps to 5000 on current meshes.
Question: does the amount of illegal cells (in this case non- orthogonal cells) that are recorded after the mesh is created, affect the simulation? As in, do the solvers treat the discretisation of these cells differently based on how many are reported as illegal, or do the solvers treat based on the actual degree of non-orthogonality
Sorry for the long post, i have a bad habit of doing that haha
Dan
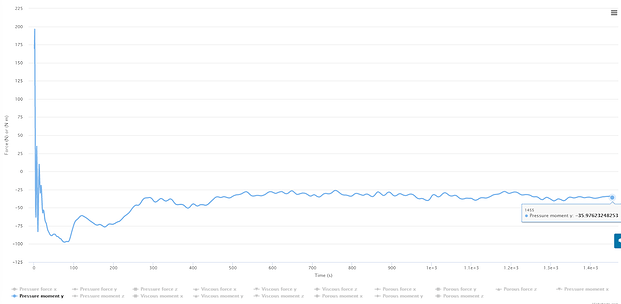
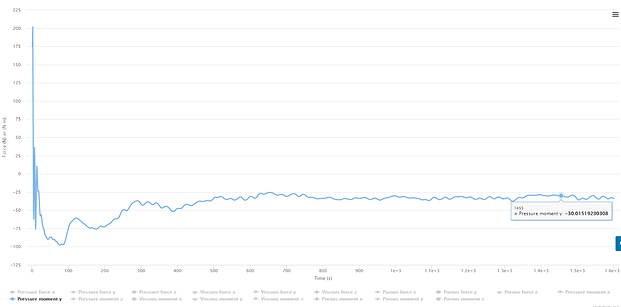
(6 more if you want viscous too)
