I would like to start a new thread about simulations of Porous Media. I have already gone through other threads and projects, as well as other research but i feel that there is not a very clearly stated instructions on how to perform this simulation type, specifically for an FSAE car radiator.
Edit!! I was unaware of these article in Simscale that perfectly describes this process!!
Simscale documentation > Knowledge Base
Through this thread i would like to solve the following:
- The correct Darcy-Forchheimer equation and how to use it.
- How to calculate intrinsic and inertial permeability coefficients
- Where the source of information for the above mentioned calculations comes from
- Understanding the specific simulation condition to achieve correct results
My status so far:
Source of Equations from OpenFOAM: DarcyForchheimer - OpenFOAMWiki
The Darcy-Forchheimer Law states the following:
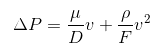
Where:
D is the Darcy coefficient - Also known as Intrinsic permeability
F the Forchheimer coefficient - Also known as Inertial permeability
Simplifying this equation we get:
![]()
From here we need to input our values from the pressure drop VS Velocity curve.This can be made in Excel from the raw pressure drop VS velocity data.This data should be given to you (or asked for) from the radiator manufacturer.
Ric has recently sent me an amazing video on this topic Fluid Mechanics 101: Porous Media
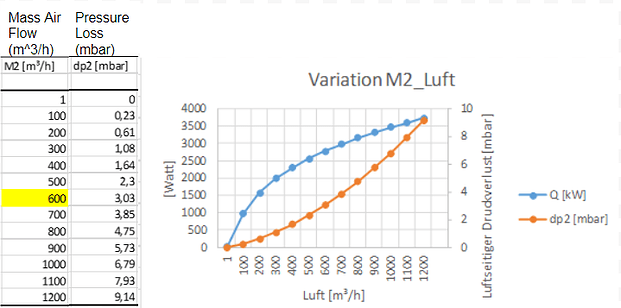
In our case, the manufacturer AKG did a workshop with our FSAE team and also provided simulation software for the radiator. This provided the following data.
In my situation, the Mass air flow is in meters cubed per HOUR. This means it is important to check your units so that the results make sense. Since we need our Mass air flow in M^3/S we must divide the data by 60 to get minutes then 60 again to get seconds. Using Excel makes short work of these calculations by using an equation to relate the MAF data input. Then dragging this equation down, calculates each result using each new input.
Now using Mass Air Flow in m^3/s we need to convert the mass airflow into velocity using the following equation.
![]()
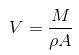
ρ: Density of the gas, in kg/m^3
V: Flow speed, in m/s
A: Flow area, in m^2
M: Mass flow rate, in m^3/s
Using excel, we can equate this conversion to get our final Velocity in (m/s) Vs Pressure Drop in ¶. Pressure data was recorded in mbar so we must just multiply these values by 100 to achieve Pa.
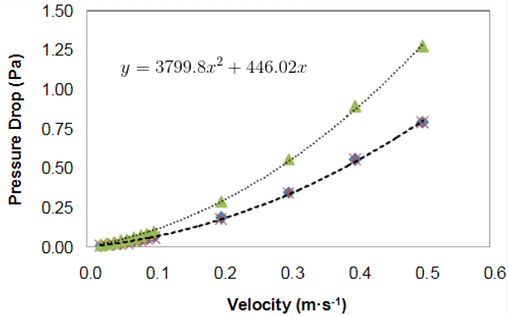
For simplicity i have used an example graph and curve equation output from hypothetical data.
The graph then outputs the velocity dependent pressure values in the example equation shown:
![]()
Switching the x and x^2 components of the equation gives us the comparison to the simplified Darcy-Forchheimer equation and lets us calculate the coefficients.
The inputs for A and B come from the curve fit equation produced from the graph
![]()
![]() Simplified Darcy-Forchheimer Equation
Simplified Darcy-Forchheimer Equation
Where
A = 446.02
B = 3799.8
Resulting in ![]()
In the case of applying this equation to porous media, the simplified variables A and B must both be devided by the thickness of the media in that specific direction. This produces the following equation:
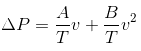
Where
T = Thickness of Porous Media (direction dependent)
Knowing the velocity dependent pressure values, we can calculate A and B and thus, the coefficients ![]() and
and ![]() can be recalculated. It should be clear, that the vectors
can be recalculated. It should be clear, that the vectors ![]() and
and ![]() can be direction dependent.
can be direction dependent.
![]()
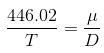
Solving for the needed coefficient D results in the following:
![]()
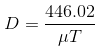
![]()
![]()
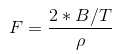
![]()
Following this procedure will give you the Darcy and Forchheimer coefficients for the porous media input parameters.
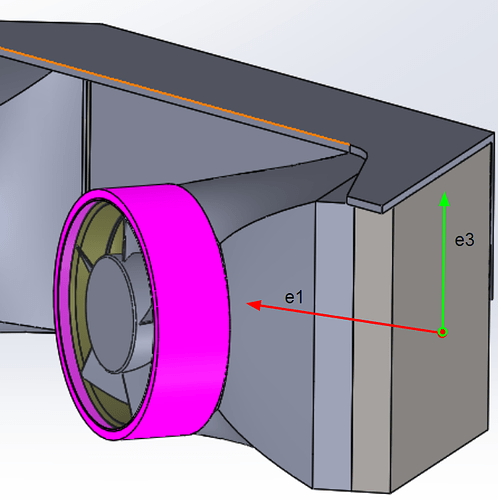
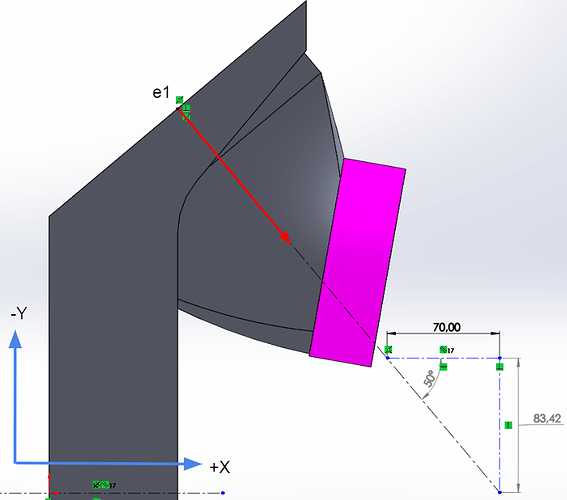
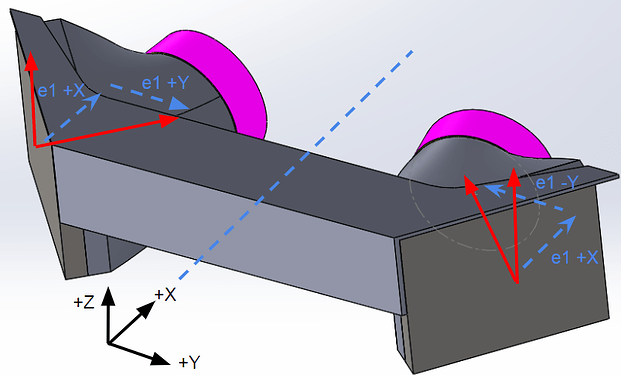
Now that we have the coefficients we have to input their direction through the vectors e1 and e3. With the flow U moving along the positive X axis, The first vector to find is e1. In the example provided by the Simscale FSAE tutorial, the radiator is tilted by a certain angle, but the front face is parallel to the Y axis, meaning there is no Y component to the e1x, e1y and e1z coordinate system. So e1y = 0.
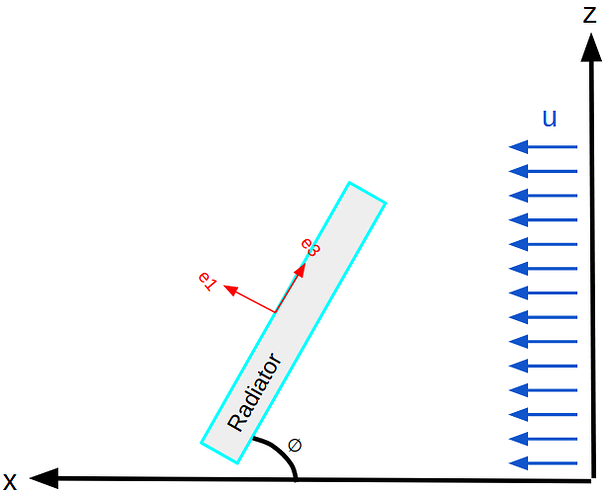
In my situation, the radiator face is parallel to the Z axis, so my e1z component will equal 0. e3, as explained in the tutorail is perpendicular to e1, so in my case e3z will equal positive 1 giving the direction in the z axis.
The e1 vector is calculated by creating a coordinate system around the point. As said above, e1z =0 because the radiator face is parallel to the z axis. To calculate the angle and direction, measurements were taken from the 3D model. The values are not important, as long as the X and Y components equal the 50 deg angle of the radiator as shown below.
Here we have a value of 70 in the positive X direction, therefore e1x = 70. With an angle of 50 deg, this creates a Y component value of 83.42. By leaving this value positive, it determines that the radiator face is pointing towards the centerline in the +Y direction. For the other side of the car, in a full car simulation, this value must be negative to show the radiator face is pointing in the opposite direction.
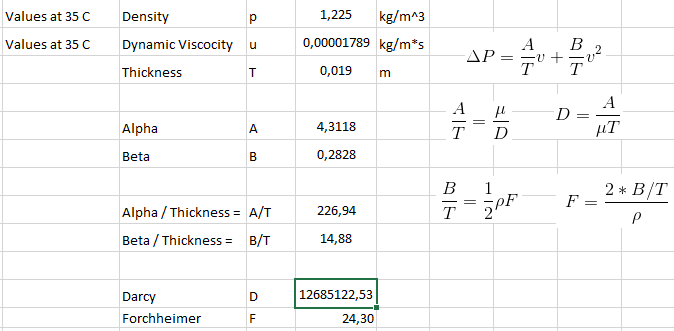
How to create a Curve fit graph for Darcy-Forchheimer calculations in excel
In order to calculate the coefficients, we must relate our pressure drop VS velocity data to a second order polynomial. This can be done easily through excel.
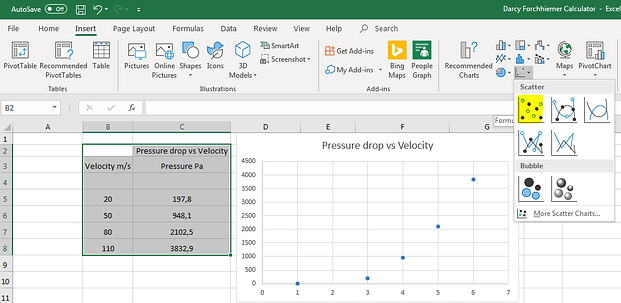
- Input the data as shown below in two columns with a title. Then select the whole data set and input a scatter plot graph.As you can see our pressure data is represented on the vertical axis but velocity isn’t,
- Simply select the data set on the graph and drag the purple and blue boxes to represent only the numerical data. We now have our data plot.
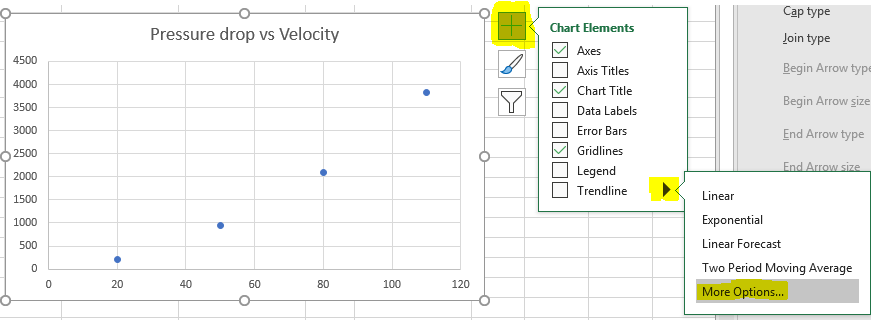
- Then under the + tab selection next to the graph, select the arrow under trendline then more options.
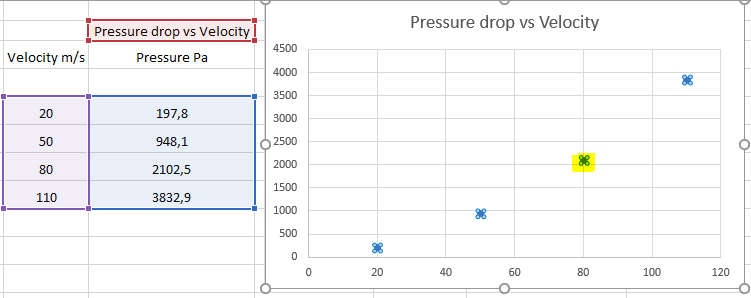
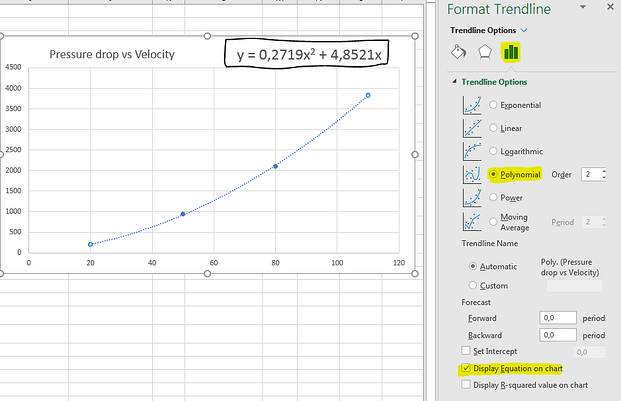
- Navigate to the three bars under trendline options. Select Polynomial for line type. Then select Display Equation on chart. You will now see the function that is used to relate the Pressure drop VS Velocity data to the Darcy-Forcheimer equations. In this case Alpha (A) is 4.851 and Beta (B) is 0.2719.
- Adding the equations and relations between them into excel helps to further automate this process.
Good Luck!
Obtaining pressure and velocity data from self-made Radiator Simulation
It is also possible to simulate the pressure drop using the real radiator model and achieve the Pressure Vs Velocity data. To set up a simulation. First create a wind tunnel that completely encloses the radiator porous zone.
Simplified radiator Geometry with border
Bounding Box Encloses radiator porous face
The best method to measure pressure drop across the radiator fins is with the viscous sublayer (Y+< 8). Due to the small size of the fins and the space between them, the shear forces are the greatest factor for this pressure drop. There is undoubtedly inertial forces at play, but any boundary layer formed in these tight areas, and over such a small distance (20mm thick) will be mostly laminar and not turbulent flow. My simulations are run using the K-Omega SST model but using full resolution (for laminar flow Y+=< 8) and not wall functions (for laminar approximation and turbulent flow - Log-Law region 30 <Y+< 300).
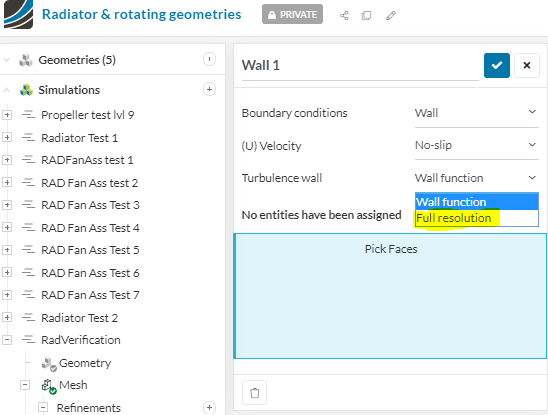
Pressure Drop Data selection
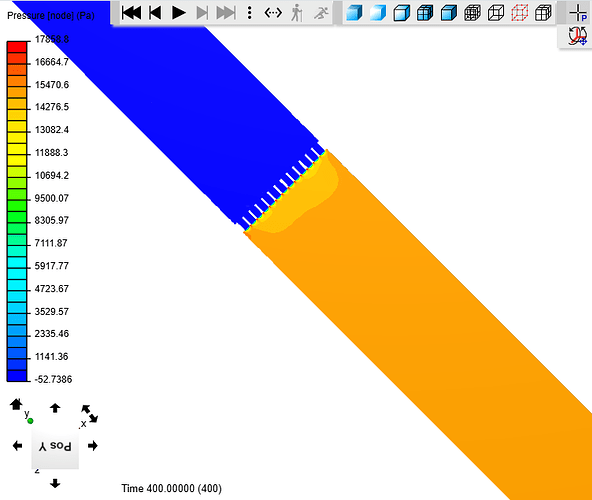
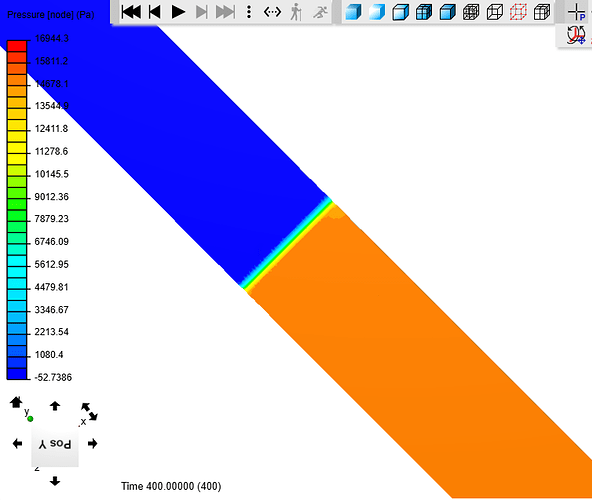
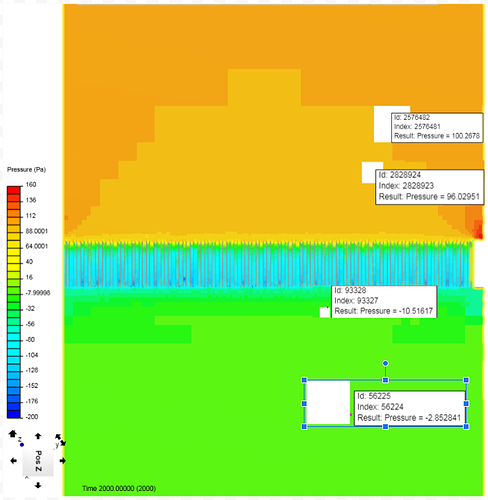
After the simulation is complete and Y+=< 8 values are verified, the resultant should look something like this.
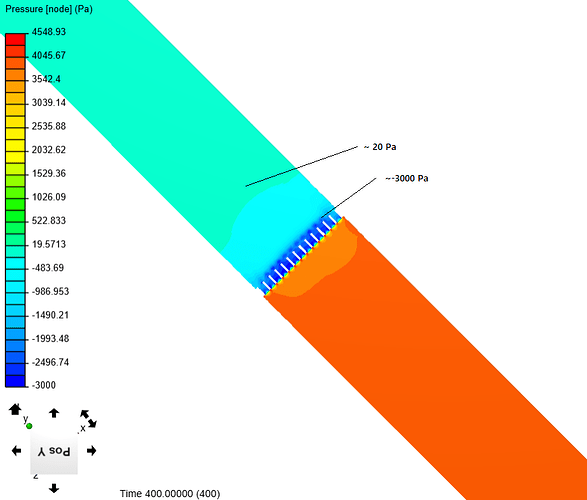
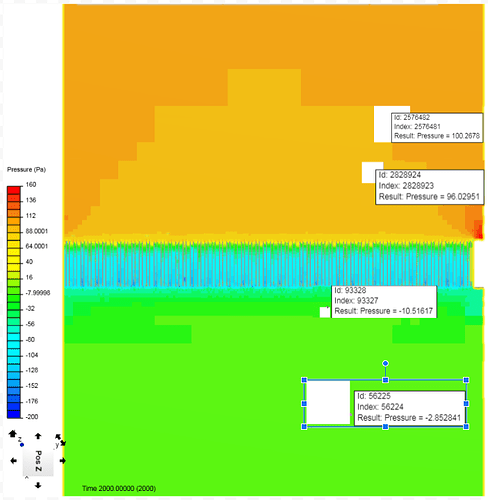
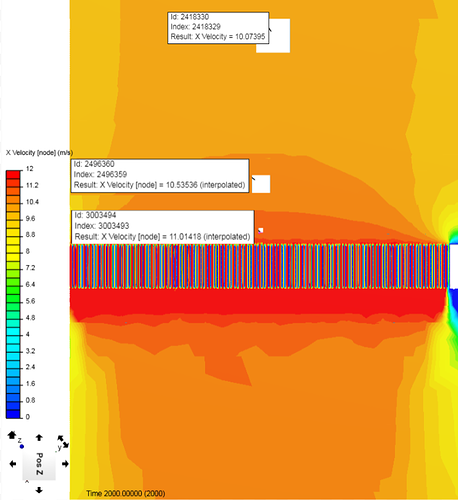
Upon closer inspection the pressure zones can be identified.When a slice is made through the middle of the radiator, you can use the “Select Element” tool from the top toolbar in Simscale. This allows you to click on every HEX prism and find the node data from that point.
My overview slice of the radiator shows
Dark Orange ~ 100Pa - inlet starting pressure at 10m/s velocity setting
Light Orange ~ 96Pa - pressure starts to drop as the air speeds up to pass through the restrictive fins (Bernoulli effect)
Dark Green~ -10Pa - pressure drop after passing through the radiator - pressure recovery zone
Light Green ~ -3Pa - Final pressure difference
The data to be collected is going to be the pressure values that are present upstream and downstream of the radiator. This will give us the total pressure difference of the system. Data taken too close to the radiator will give an incorrect representation of the results. This is best said by Ricardopg later in the thread.
“If you make a slice immediately downstream of the porous zone, this area is most likely going to have the lowest pressure fields. As you go a little bit further downstream, flow recovers some pressure as it readjusts (Bernoulli).For the porous zone formulation, pressure drops are permanent - there’s no recovery. So if you don’t take the aforementioned recovery into account, you will most likely end up with a pressure drop that is bigger than the one you would expect.”
So our pressure drop data to be used in this case, would be:
Starting Pressure 100Pa - Ending Puressure -3Pa for a total difference of 103Pa
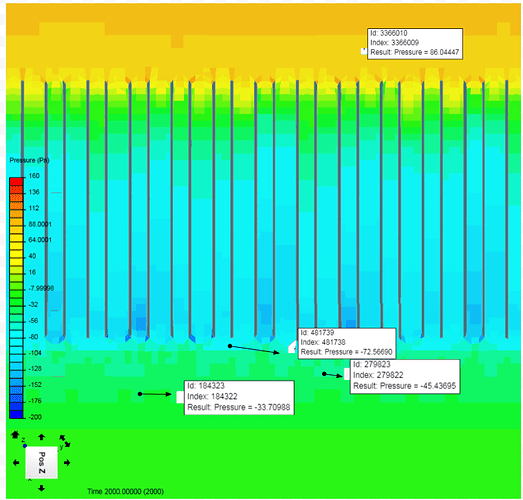
Velocity Data selection
Now for the velocity data, based on the video earlier in the post, the data should come from the air speed directly in front of the radiator face. This is shown below. Again the “select element” tool is used to collect the node data. We see here that our starting inlet velocity is 10m/s and continues to increase before the radiator face as the air speeds up. We will be taking the data from the dark orange area, which has increased to about 11m/s.
Velocity profile
We now have our first input for our Pressure drop vs velocity data set. By simulating at multiple speeds we can get a range of values to be used in the Excel program to calculate the Darcy-Forchheimer coefficients.
| Pressure drop Pa | Velocity m/s |
|---|---|
| 103 | 11 |
Please comment on the equations and methods i have listed above. I want to know if what i am doing is accurate or even correct.
I will upload results once i get the velocity VS pressure drop data from the manufacturer.
Thanks, Dan



 Thanks a ton for your efforts
Thanks a ton for your efforts