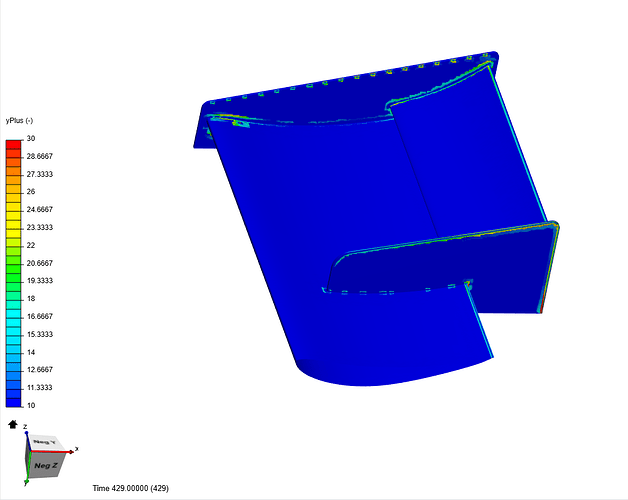
Yup @Lwhitson2 is absolutely correct about the yplus value for k-omega SST model. The shear stress transport (SST) k-ω model is a two-equation model that combines the advantages of the k-ε and k-ω models. This model uses a blending function to gradually transition from standard k-ω in the inner boundary layer to standard k-ε in the outer boundary layer. The standard k-ω model performs better in the near-wall region while the standard k-ε performs better in the free-stream region.
Also, there are not much cells with yplus between 10 &30.
These Wall treatment method are used by some other CFD software. Just wanted to share this with you guyzz.
7 Likes
@DaleKramer you’re never going to get a perfect Y+ value everywhere on your model. The key is to get Y+ correct in the most important parts of the flow. Overall I think the Y+ looks really good on this simulation after @anirudh2821998 made his updates to the mesh.
4 Likes
Yes but I do not think I could easily see that from Ani’s first Y+ mapping presentation. The second mapping of 10<Y+<30 does confirm this for me.
Very good Ani !!!
EDIT: And just to confirm, this will be a Full res Y+ simulation, correct?
also, I like to show mappings like that with a Grey area for Y+<10 , I know we can do that I just don’t remember off hand how I did it, or Y+<1 like this:
1 Like
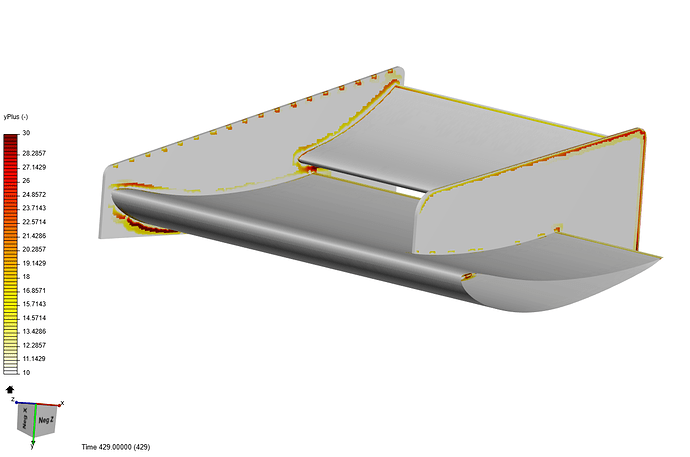
Sir, Is this what you are suggesting??
Not really, I added an example while you were posting, it still shows rainbow 1 to 10
Well, there is a white to brown color scheme but I can’t see any raibow type color scheme. Did you use some other post processing tool?
I don’t believe so but it was with old workbench, maybe can’t do this anymore…
I did add the ‘Gray is y+<1’ text in an image processor tho.
Hello Ani,
For this inflation layers parameters you used relative layering?
And this layer calculation is for a full resolution right?
Did you just changed the inflation layers parameters?
Would it be good to alter the surface refinement level, region refinement level or the bounding box resolution in Ani´s mesh to have a smoothier transition from prism cells to region cells?
No
Yes
I just modified the size of the bounding box(made it a bit larger) and changed only the inflation layer parameter.
It is a must to simulate your problem with atleast 2 different quality mesh. This will provide you with an idea of the deviation in results with mesh fineness and will also serve the purpose for mesh independence study.
1 Like
To add to this, I would suggest running a full grid convergence study using at least three grids and verifying the order of convergence for your model. This would satisfy the scientific/research level requirements and is great experience to have in validating your model. Here is a link to a great article by NASA that will help you in the calculations. Near the bottom is an example of the grid refinement study.
Examining Spatial (Grid) Convergence
4 Likes
I have some questions about the layer refinement. In this mesh you did, what value of Y+ were you aiming? And what value of expansion rate you used?
@math_marques96 it depends on what turbulence model you plan on using. I would start with the \kappa \text - \epsilon model and target a y^+ of about 50 with a growth factor of around 1.2 - 1.3 and a last layer thickness somewhere around 83\% of your standard surface mesh size. After running a few cases with \kappa \text - \epsilon you will know whether or not separation is an issue. If so, I would switch to the \kappa \text - \omega\,SST model and then target 1 \leq y^+ \leq 5 in the areas where the separation occurs.
The first model will get you about 90\% of the way there and the second will get you that last 10\%. It all depends on your time requirements and what you are looking to get out of the simulation.
3 Likes
Hello,
I made some changes in the layers refinement and acquired a better mesh. I am in doubt about a layer parameter.
I found this forum Boundary layer inflation thickness - #4 by AnetaNovak and it was not clear for me if what parameter is the “final layer thickness”. On this forum there is also a “first layer thickness” parameter that not appear in my simulation.
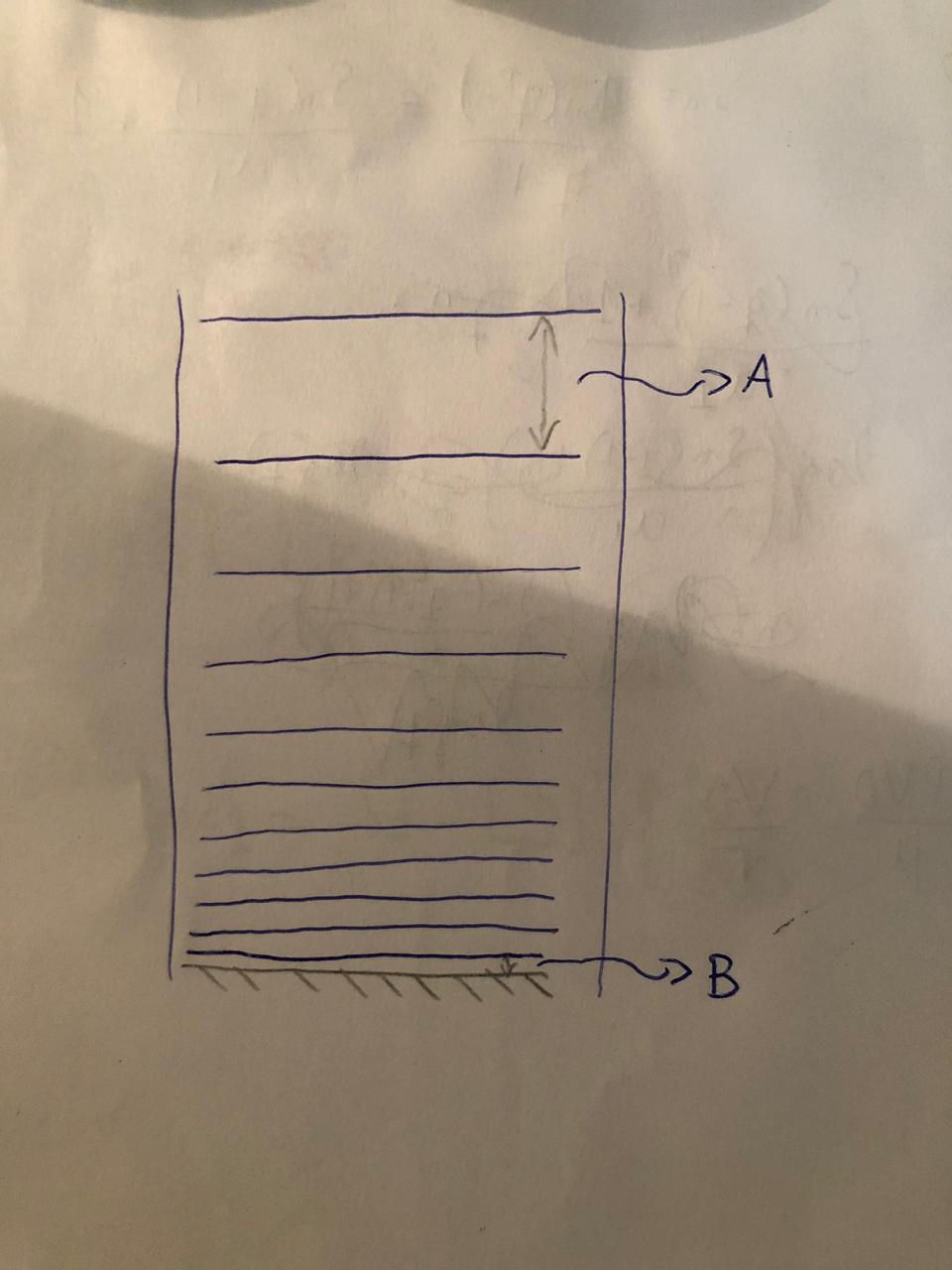
I uploaded this draw of a boundary layer, to show my question, the parameter “final layer thickness” is the A or B? Is it possible to choose between using the “final layer thickness” or “first layer thickness”, I did not understand if it is the same also.
Thank you very much!!
In my simulation, the “final layer thickness” parameter appears. Is it possible to I select the “first layer thickness” parameter instead? I am not finding where I can select this option.
Our PowerUser @anirudh2821998 has posted a good procedure for this here: Boundary layer inflation thickness - #3 by anirudh2821998 - if anything is missing for your calculations, please let us know and we will fill this gap!
Best,
Jousef

I read the post and did not find where can I change the “final layer thickness” to the"first layer thickness". This is what shows in my simulation:
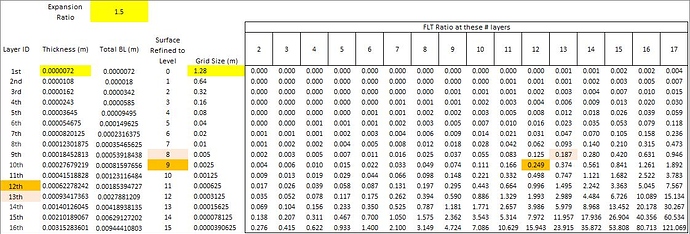
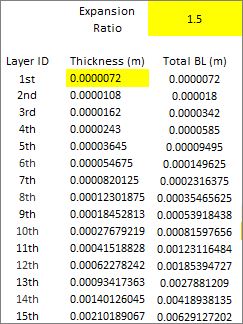
That is impossible to do, you must create a table like this (and you have to read and understand how the mesh parameter ‘Layer Size’ affects the value of what you enter in the ‘Final Layer Thickness’ (FLT) parameter):
If ‘Layer Size’ is ON (also known as Relative Layering), then FLT is a dimensionless Ratio of the final prism cell size to the adjoining volume mesh cell.
If you choose to use Relative Layering (I do) then you need a further table that lets you pick your FLT ratio based on the surface level refinement, which you choose to refine all the faces that you are putting a boundary layer on (I generally use an FLT ratio of ~0.2 to ~0.4 but that is not a hard rule):
If ‘Layer Size’ is OFF, then FLT is an absolute thickness in meters of the final layer that touches the volume mesh cell.
1 Like
Hi @math_marques96
Here are the steps to make the desired number of inflation layers
-
Use any y+ calculator to get the value of first layer(nearest to wall). Just feed in some values asked by the calculator and you will get the suitable thickness of first layer. I prefer to use this calculator- http://www.pointwise.com/yplus/
-
Decide a suitable expansion ratio and number of inflation layers. Then determine the thickness of farthest layer —a*(r^(n-1))
a= first layer thickness, r=expansion ratio and n= number of layers
-
Check whether relative sizing option is on/off. I usually prefer my relative sizing option to be off.
Thanks
Ani
3 Likes