Well, I’m sorry to say that buckling analysis is not currently available in SimScale.
To study other failure modes such as local yielding and global yielding you can use non linear analysis simulation.
1 Like
Ok, I will take a look at that, thank you
About the buckling, knowing that is not available in SimScale, what would be your advise about this? Is there any calculations I might be doing as an aproximation, or it just should be done by FEM analysis?
I took a quick look at your project. Here are some points that you might find helpful (not related to your original question).
- You are using a first order mesh. You will get much more accurate results with a second order mesh.
- You have not included the load due to gravity. This can be added under Model in the project tree.
- The small radii in your model are not necessary. They just add computation time and have very little impact on the result.
- For symmetry, where possible, you should use “Fixed Value” and pick one direction (X,Y or Z) as this is more robust than the “Symmetry” option (which can work at angles other than the three orthogonal directions).
The image below shows the difference these changes make.
With regards to your original question. A frequency analysis is sometimes useful in assessing the “stability” of a structure. A frequency analysis will tell you the eigenfrequencies of the structure and their corresponding shape. In general you want the first mode eigenfrequency to be as high as possible. This will result in a stiff structure.
In this application you could think of a frequency analysis as a tool to identify any weaknesses in the structure that may not be in the primary load direction.
Here is a copy of your project where I have run a frequency analysis.
https://www.simscale.com/projects/BenLewis/steel_ring_v2/
The first mode natural frequency of your structure is 14.5 Hz. The image below shows the shape.
This could be improved by moving the leg brace further up the post.
6 Likes
So useful information. Thank you very much
So,
- The gravity load: This is because first I was using this tool:
https://www.xcalcs.com/cgi-bin/tutti/x3calcs.cgi?a=tf&d=i_0_4_1_0&l=en
So I calculated the total weight (lead to support + own steel beam). Then, I will remove the steel contribution from the external pressure. I guess this is much better like this, thank you
-
About the radii. As it is the problematic zone, I thought it would be better to do the most real. I will look at it
-
Frecuency analysis: Ok, I am not familiar with frequency analysis, so I will take a read. However, how can you estimate that 14.5 Hz means a low value?
Again, thank you for all,
cheers
Sometimes it is important to include the radii, especially if the sharp corner creates a stress singularity. In general I start with no radii and only add them when required. If in doubt, a mesh convergence study can help identify singularities.
Actually from what I know of your application a first mode natural frequency of 14.5 Hz is pretty good. This is quite a stiff structure. I was simply pointing out that a frequency analysis can be used to find the most flexible part of the structure.
If, for example, you had designed the structure without the diagonal leg braces, the maximum stress under load, in a static analysis, would be no different to what is is now. But the first mode frequency would be be much lower (e.g. 1 Hz). Intuitively you knew to add bracing in this direction even though the static stress analysis does not require it. In some cases the required bracing is not so obvious. This is where a frequency analysis can help.
The required minimum natural frequency is highly dependent on the application. If the structure is subject to large cyclic loads and good dimensional control of the structure is required then the first mode natural frequency may need to be as high as eight times the frequency of the applied load (rule of thumb).
Sometimes it is important to have a low natural frequency. For example, earthquake resistant buildings are designed to have a low natural frequency. During an earthquake the structure will move large amounts and non load bearing members will intentionally undergo large plastic deformation to absorb energy. If the structure is too stiff it will fail catastrophically because there is no capacity to absorb energy.
If, on the other hand, none of these factors are important then the minimum natural frequency becomes a bit arbitrary. You have to look at the frequency and shape and make an assessment about whether or not you think the structure is stiff enough in that direction.
4 Likes
Hello @BenLewis, ok I get the point
I have been reading about modal and frequency analysis, now I understand it much better. However, I still have two concerns:
- First mode frequency means the first natural frequency, so it is the lower frequency in which the structure could resonate, which would occur only If the external loading have the certain directions for this mode or shape.
Ok so then, why 1 Hz would be more dangerous than 14 Hz? Is it because it is “easier” to have a low frequency oscillation in the external load? Because, the more the frequency, the more improbable to occur in the real world. Is it the reason?
- Does Simscale show the shape of each mode of vibration? (I have not found it)
That way one could try to predict which of these modes are likely to happen, or which ones are not going to happen, due to the external loads directions.
Thank you very much, so helpful
A 1 Hz structure is weaker (more flexible) than a 14 Hz structure.
In this video you can see that the more slender (weaker) structure has a lower natural frequency.
It this context it is not so much that the higher frequencies are less probable.
Yes, SimScale can show multiple mode shapes. Each mode is accessed as a time step. Here are the first 4 modes. Modes 3 and 4 relate to your original concern about having a slit in the ring beam. These frequencies are very high meaning the structure is stiff (strong) in this regard.
When doing a frequency analysis you need to ensure you are using the correct mass. From you description it is not clear to me it your structure is carrying a mass other than its self weight. If it is, this needs to be taken into account. Adding mass to the structure will lower its natural frequency.
4 Likes
Great video, very self explanatory
So then, If I understood correctly:
For the experience, we know that higher (then, more flexible) structures have a lower resonance frequency. So then we can attest that If modal simulation returns a lower first frequency, that means the structure must be weaker than if it returns a higher first frequency. Even If the weaker one could support better some “higher range” frequency than the less weak
Ok about the mode´s graphics display…I have been looking around the post-processor, and still not able to locate the feature, Im sorry
About the mass: Here you can see the application:
Lead will go inside (grey color), it´s about 13 tons of weight. But the load is already applied (see SimScale )
On the other hand, I must say that I run two static analysis: with and without radii. There is a big difference: 86 Mpa vs 50 Mpa)
Thank you for everything
Online post processor
The mode can be selected via the time/frame control. Unfortunately, the online post processor defaults to the highest mode instead of the lowest mode, which is probably counter intuitive for beginners.
ParaView
I recommend using ParaView. With Paraview you have two options. You can load just one mode by selecting the appropriate vtk file.
Alternatively, you can load all modes by selecting the top level group.
The the displayed mode can be controlled with the appropriate time step.
For a frequency analysis it is not correct to replace the mass with an equivalent force. You will need to add the mass, especially because the mass is so substantial.
You could get a rough approximation by changing the material density to achieve the equivalent mass.
Yes, in some cases a radius is important. Sorry to have led you astray here.
In your project I noticed you are using a half model for the frequency analysis. A half model cannot be used here because not all modes are symmetric.
4 Likes
Ok so then:
-
I will experiment with ParaView
-
About the mass: Yes, I know, I am not using any load for frequency analysis, I was referring to the static one. I know modal results are only dependent of geometry and constraints.
However, you say I should recalculate density ? So I should be raising it from 7870 kg/m3 (steel) to 55000 kg/m3 ?? (15 tons/volume of structure)
I did not do this because modal analysis is independent of external loads, and lead (12 tons) is actually an external load. So the density should be about the steel structure, no matter which load you put on top of it
-
About the radii, it´s ok as it´s good to know as well
-
Ok I will not use symmetry for modal. If you see, there are a full geometry analysis and half geometry analysis with symmetry, and both return the same first frequency, that´s the reason I was using it
Thank you
You should add the lead mass to the model to get accurate frequency results. You can “cheat” by changing the density of the structure to achieve the same effective mass. This will give you a rough indication of the first mode frequency without having to re-mesh the model. Your calculation of the required density is correct:
effective density = ((m_struct+m_lead)/V_struct).
Natural frequency (omega) is dependent on two factors - mass (m) and stiffness (k):
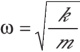
If the structure is carrying a mass then it must be included in the calculation of natural frequency.
Here is another video that might help convey this concept.
If you are concerned that the lead mass should not add to the stiffness of the structure there are ways to deal with that.
2 Likes
Understand. So I am dealing with an error during the simulation when using the full geometry, but I am contacting the support
You have been so helpful. I will post the results when I get it simulated. I assume some first natural frequency of 14 Hz should be good enought
When you add the lead mass I expect your first mode frequency will drop to around 6 Hz. If you hit this structure with a large mallet you would expect to feel a vibration at this rate.
The frequency analysis has showed you that your structure is weakest in the for-aft direction. You have no dynamic loading to consider so, so long as you are comfortable that your structure is adequately braced in this direction, 6 Hz should be fine.
Understood. I am waiting for the results as I am not able to compute the analysis for some errors. Hopefully the official support can help me
About the mallet, you mean If you hit it during some period of time at 6 Hz frequency? Or just one hit?
As I understand from the videos, that frequency must be continuous, like the vibration of the support in the SDOF resonance test
I made a copy of your most recent project and made some small changes to fix the error. You can see it here.
The first mode natural frequency is now 7.6 Hz. It is slightly higher than I expected because the outer leg braces have been made larger.
It is only necessary to hit the structure once. If you put your hand on the structure you will feel it vibrate for a brief period of time. If you instrument the structure (with accelerators, displacement transducers, strain gauges etc) you will see a vibration signal. This vibration can be broken down into its constituents. All of the frequency modes will be present but in varying amplitudes. Typically the first mode is largest and subsequent modes get progressively smaller. This is called free vibration. A mass on a spring is an example of a free vibration.
What you are seeing in the SDOF video is an example of forced vibration. The shaker table forces the structure to vibrate at a given frequency. It starts slow and progressively gets faster. When the rate of forced vibration matches the natural frequency of the structure the structure will resonate.
3 Likes
Thanks a lot for the explanations and also for the fix in the project
Then we have a first mode natural frequency of 7.6 Hz which seems to be fine.
However, I will need to make a report including the sources in which I have been based. I have not found any document in which relation between frequency and stability is explained. I understand you are based in your own experience and I do not doubt about it, but do you know where can I find further information so I can contrast the results with some written sources?
Thank you
Sorry I don’t know of any references.
Please keep in mind that the first mode frequency is not a measure of the structure’s stability (i.e. resistance to buckling or over turning). It is a measure of the structure’s flexibility. You can use the fact that the first mode is the structure’s most flexible mode to make some assessment about whether the structure is adequately braced in this direction.
In your application there appears to be sufficient bracing in the first mode direction. If you need to verify this then you will need to perform a non-linear analysis. A non-linear analysis will tell you what horizontal force is required to push the ring beam over to the point where is becomes unstable (if at all). I don’t believe this is necessary, I’m only mentioning it so that you understand what could be done if it was required.
1 Like
Yes, I understand frequency analysis in only about determinating the most flexible “direction” or vibration mode
About the non-linear analysis, I do not think it is necessary neither. Just because there will not be any horizontal force pushing the ring.
However, I actually would like to know how to do it. I already made some non linear analysis, but not considering any horizontal force, only the lead weight. That returned me the same results as linear analysis. So for verifying the pushing horizontal force needed I would need to play with horizontal loads right?
Thank you for everything. Already been so helpful
For a non-linear analysis you will need to make the following changes to your current half model linear project:
- Change to a nonlinear simulation type with
Simulation > Properties > Nonlinear analysis > True - Enable geometric nonlinear behavior with
Model > Geometric behavior > nonlinear - Enable nonlinear material behaviour with
Model > Materials > Steel > Material behavior > Plastic - Add a table to define the materials stress-stain curve after yield. You can find examples here
- Add a time dependent load e.g. 10000*t
Model > Boundary Conditions > Loads - Enable line search to give the solver a better chance to find a solution in the post buckling region.
Numerical > Line Search > True
I may have forgotten a few steps but that’s probably enough to get you started.
Give it a go. If you have any trouble please let me know and I will see if I can help.
3 Likes
Of course…I will try during the week
And I will give the results here. Thanks!