Validation Case: Infinite Cylinder Subjected to a Volume Load

This validation case belongs to solid mechanics. In this case, an infinite cylinder is subjected to a voluminal load. The parameter being validated is:

Volume load

SimScale simulation results were compared to the analytical solution presented in [SSLA100] $^{1}$ .

View Project

Geometry

The geometry for this project consists of a slice of an annulus between two cylinders, as seen in Figure 1:

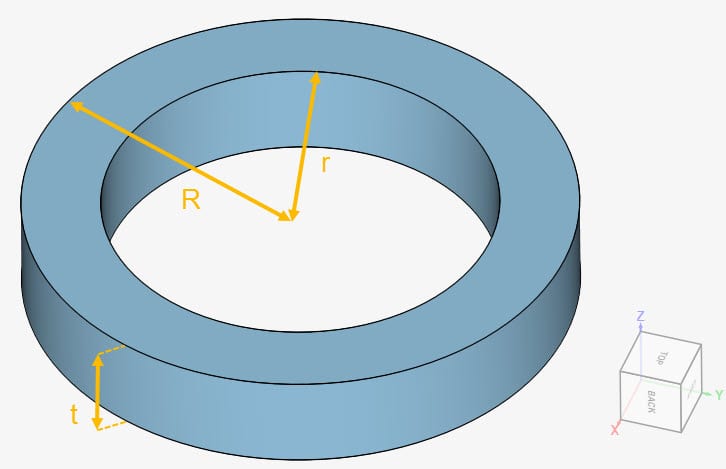
infinite cylinder volume load validation case — Figure 1: Slice of an annulus, used in the present validation case. The centroid of the annulus has coordinates (0, 0, 0).

The dimensions of the geometry are given in Table 1:

Geometry parameters	Dimension $[m]$
Outer radius $(R)$	1.4
Inner radius $(r)$	1
Thickness of the slice $(t)$	0.5

Table 1: Dimensions of the concentric cylinders

Analysis Type and Mesh

Tool Type: Code_Aster

Analysis Type: Linear static

Mesh and Element Types: The mesh used in this case is a second-order mesh created in SimScale with the standard algorithm.

Table 2 contains details to the resulting mesh:

Mesh Type	Nodes	Element Type
Second-order standard	991445	Standard

Table 2: Second-order standard mesh characteristics

Figure 2 shows the standard mesh used for this case:

annulus between two cylinders validation case — Figure 2: Discretization obtained with a second-order standard mesh

Simulation Setup

Material:

Material behavior: Linear elastic
Young’s modulus $E$ = 10 $P a$
Poisson’s ratio $ν$ = 0.3
Density $ρ$ = 1 $k g / m ³$

Boundary Conditions:

The boundary conditions will be defined based on the following nomenclature:

Constraints
- $d_{z}$ = 0 on both sides
- Isotropic elastic support applied to the inner wall, with a spring constant $k$ = 0.001 $N / m$ . The purpose of this boundary condition is to avoid rigid body motion.
Surface loads
- Pressure of 1 $P a$ applied to the inner wall
- Volume load applied in the radial direction, with a magnitude of $α r^{2} (\frac{N}{m^{3}})$ , where $α = 1 \frac{N}{m^{5}}$ and $r$ is any given radius, in meters.

forces applied in a radial direction — Figure 4: Volume load applied in a radial direction. The magnitude of the load is radius squared.

Note

Since the volume load is in cylindrical coordinates $^{1}$ , it was necessary to convert it to Cartesian coordinates using trigonometric functions. The resulting input formulae are:

$\begin{matrix} (1) & L o a d_{x} = (x^{2} + y^{2}) c o s (a t a n 2 (y, x)) \end{matrix}$

$\begin{matrix} (2) & L o a d_{y} = (x^{2} + y^{2}) s i n (a t a n 2 (y, x)) \end{matrix}$

$\begin{matrix} (3) & L o a d_{z} = 0 \end{matrix}$

In equations 1 and 2, the $(x^{2} + y^{2})$ term represents radius squared. The second part of the equations, consisting of trigonometric functions, is responsible for the conversion from cylindrical to Cartesian coordinates. As a result, the loads will be applied in a radial direction.

Result Comparison

The analytical solution for the displacements of the inner and outer wall are presented in [SSLA100] $^{1}$ . Find below a comparison between SimScale results and the analytical solution:

Radius $[m]$	Analytical displacement $^{1}$ $[m]$	Displacement – SimScale $[m]$	Error [%]
1	0.521309	0.521259	-0.0096
1.4	0.442031	0.441986	-0.0102

Table 3: Comparison of SimScale results with the analytical solution

In Figure 5, we can see the resulting displacement contours. SimScale results show great agreement with the analytical solution.

volume load displacement contours — Figure 5: Displacement contours obtained with SimScale

References

“SSLA100 – Infinite cylinder subjected to a field of voluminal and surface forces”

Last updated: September 4th, 2023

Did this article solve your issue?

How can we do better?

We appreciate and value your feedback.