websights

Fill out the form to download

Required field
Required field
Not a valid email address
Required field
Required field

  • Set up your own cloud-native simulation in minutes.

    • Documentation

    SimScale DocumentationValidation CasesValidation Case: Random Vibration Analysis of a Cantilever Beam

    Validation Case: Random Vibration Analysis of a Cantilever Beam

    This validation case belongs to solid mechanics. It aims to validate the random vibration response of a square cantilever beam, where the beam is excited by the Base excitation boundary condition in SimScale Harmonic analysis solver.

    The simulation results from SimScale were compared to the reference results presented in results in [Johnsen and Dey (1978)]\(^1\)

    View Project

    Geometry

    The geometry used for the case is as follows:

    square cantilever beam geometry that is used for random vibration analysis in simscale
    Figure 1: Geometry model of the square cantilever beam

    The dimensions of the geometry are tabulated below:

    Geometry ParameterDimension [m]
    Length (L)1
    Width/Height (X)0.1
    Table 1: Dimensions of the square beam

    Analysis Type and Mesh

    Tool Type: Code_aster

    Analysis Type: Harmonic Analysis

    Mesh and Element Types:

    The meshes were computed using SimScale’s standard mesh algorithm and manual sizing. The following table shows an overview of the mesh characteristics:

    CaseElement TypeNumber of NodesElement Technology
    A1st Order Tetrahedral32 663Standard
    B2nd Order Tetrahedral118 696Reduced Integration
    C2nd Order Tetrahedral240 757Reduced Integration
    Table 2: Number of mesh nodes and types of elements for each case.
    a meshed square cantilever beam in simscale
    Figure 2: Tetrahedral mesh for the beam, in this case corresponding to case C

    Simulation Setup

    Material:

    • Linar Elastic Isotropic
      • \(E\) = 210 \(GPa\)
      • \(\nu\) = 0.3
      • Hysteretic damping
        • Hysteretic coefficient = 0.05
      • \(\rho\) = 8000 \(kg/m^3\)

    Boundary Conditions:

    Random vibration analysis tests the response of a structure under a vibrating load. For practicality, this analysis uses the PSD (Power Spectral Density) curve to determine the peak responses of the structure.

    • Base Excitation:
      • The whole structure is subjected to a fixed acceleration of 1 \(m/s^2\) along Y-axis.
    description of the random vibration analysis on a cantilever structure in simscale
    Figure 3: Base excitation applied on the cantilever on Y-axis

    The base excitation is applied as an acceleration (1 \(m/s^2\)) in the Y-axis together with the Power Spectral Density (PSD), which is presented in the following table:

    Frequency [Hz]PSD acceleration [g^2/Hz]
    200.02
    520.053
    9000.053
    20000.0022
    Table 3: Power Spectral Density of the base acceleration

    Reference Solution

    The reference solution comes from the analysis of Johnsen and Dey (1978)\(^1\). The published reference data covers the Response Power Spectral Density (RPSD) of the displacement at the tip of the cantilever. In SimScale, acceleration at the tip of the cantilever is measured and RPSD of the displacement is calculated as follows:

    First, calculate the Response Power Spectral Density of the Acceleration.

    $$RPSD_{Acceleration}= \big(\frac{a_{out}}{a_{in}} \big) ^{2} .PSD_{input} . g^2$$

    • \(RPSD_{Acceleration}\) \([m^2/(s . Hz)]\): Response power spectral density of acceleration
    • \(a_{in}\) \([m/s^2]\): Input acceleration that is defined in the base excitation (in this example 1 \([m/(s^2)]\).
    • \(a_{out}\) \([m/s^2]\): Output acceleration. This value is measured in SimScale, using a probe point at the tip of the cantilever, for magnitude of acceleration at Y-axis.
    • \(PSD_{input}\) \([g^2/Hz]\): Input PSD of acceleration, which is given in the reference.
    • \(g\) \([m/s^2]\): Gravitational acceleration

    Next, convert the RPSD of the acceleration to RPSD of the displacement, using the following equation:

    $$RPSD_{Displacement} = \frac{RPSD_{Acceleration} }{ \big(2 . \pi . f \big)^4 }$$

    • \(RPSD_{Displacement}\) \([m^2/(s . Hz)]\): Response power spectral density of displacement
    • \(f\) \([Hz]\): Frequency

    Results Comparison

    The power spectral density of the displacement at the tip of the cantilever per frequency is presented in Table 3, alongside the comparison with SimScale results.

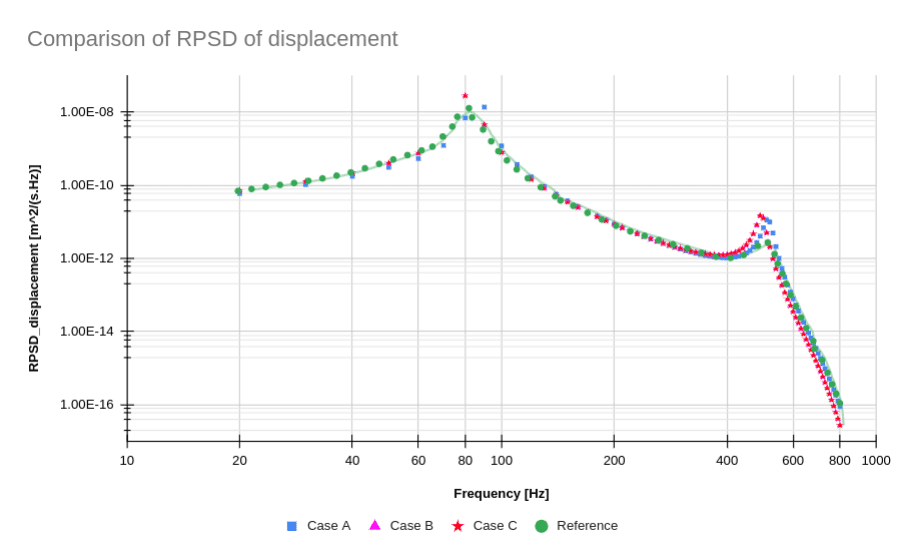
    comparison graph of response power spectral density data between reference and simulation results
    Figure 4: Comparison of RPSD of displacement between reference data and SimScale results

    The results produced are in good agreement with the reference. The frequencies at peak responses are successfully captured. The higher deviations at peaks are most probably due to the difference between the element types used between Johnsen and Dey, and SimScale.

    References

    • Johnsen, T. L, and S. S. Dey, ASKA Part II – Linear Dynamic Analysis, Random Response, ASKA UM 218, ISD, University of Stuttgart, 1978.

    Last updated: January 26th, 2023

    Contents