Validation Case: Cantilever Beam With Off-Center Masses – NAFEMS Test FV4

This validation case belongs to solid mechanics, with the case of a circular cantilever beam with two off-center point masses connected at the free end. The test case aims to validate the following parameters:

Point Mass boundary condition

The simulation results of SimScale were compared to the reference results presented in [NAFEMS]\(^1\)

View Project

Geometry

The geometry used for the case is as follows:

It consists of a straight beam of length 10 \(m\) and a circular, constant cross-section of radius 0.5 \(m\).

Analysis Type and Mesh

Tool Type: Code_aster

Analysis Type: Frequency Analysis

Mesh and Element Types:

The tetrahedral meshes were computed using SimScale’s standard mesh algorithm and manual sizing. The following table shows an overview of the mesh characteristics:

Case	Mesh Type	Number of Nodes	Element Type
A	Standard	32 663	1st order tetrahedral
B	Standard	118 696	1st order tetrahedral
C	Standard	240 757	2nd order tetrahedral

Table 1: Number of mesh nodes and types of elements for each case.

cantilever beam mesh — Figure 2: Tetrahedral mesh for the beam, in this case corresponding to case C

Simulation Setup

Material:

Linar Elastic Isotropic
- \(E\) = 200 \(GPa\)
- \(\nu\) = 0.3
- \(\rho\) = 8000 \(kg/m^3\)

Boundary Conditions:

Fixed Support:
- Face A is fixed

Point Mass:
- 1000 \(kg\) connected to face B at a distance of 2 \(m\)
- 10000 \(kg\) connected to face B at a disance of 2 \(m\)

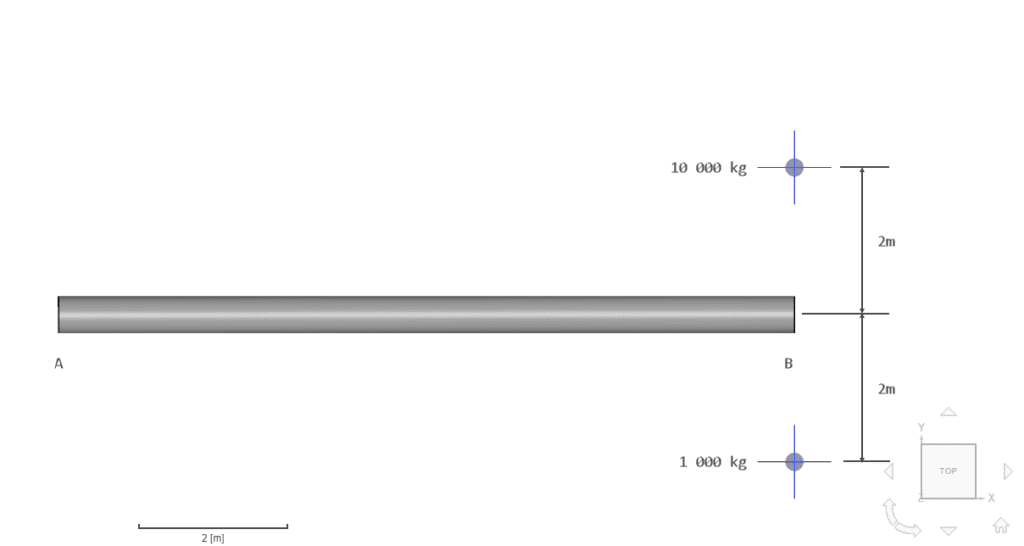
simscale validation two off-center point masses boundary conditions — Figure 3: Boundary conditions and remote point mass locations

Reference Solution

The reference solution presented in [NAFEMS]\(^1\) is of the numerical type. It is presented as the first six natural oscillation frequencies of the cantilever beam with the connected remote point mass. The values are presented in Table 2 alongside the comparison with SimScale results.

Results Comparison

Comparison of the first six natural frequencies for the run cases with the reference solution:

Mode	NAFEMS	Case A [Deviation]	Case B [Deviation]	Case C [Deviation]
1	1.723	1.739 [+0.9%]	1.731 [+0.5%]	1.767 [+2.6%]
2	1.727	1.750 [+1.3%]	1.734 [+0.4%]	1.771 [+2.5%]
3	7.413	7.573 [+2.1%]	7.448 [+0.5%]	7.593 [+2.4%]
4	9.972	10.040 [+0.7%]	9.982 [+0.1%]	10.186 [+2.1%]
5	18.155	18.344 [+1.0%]	18.141 [-0.1%]	18.524 [+2.0%]
6	26.957	26.941 [-0.1%]	26.768 [-0.7%]	27.302 [+1.3%]