websights

Fill out the form to download

Required field
Required field
Not a valid email address
Required field
Required field

  • Set up your own cloud-native simulation in minutes.

    • Documentation

    SimScale DocumentationValidation CasesValidation Case: Frequency Analysis of a Ring

    Validation Case: Frequency Analysis of a Ring

    This validation case belongs to solid mechanics. The aim of this test case is to validate the following parameters:

    • Frequency analysis

    The simulation results of SimScale were compared to the results from [SDLS109]\(^1\).

    View Project

    Geometry

    The geometry used for the frequency analysis is as follows:

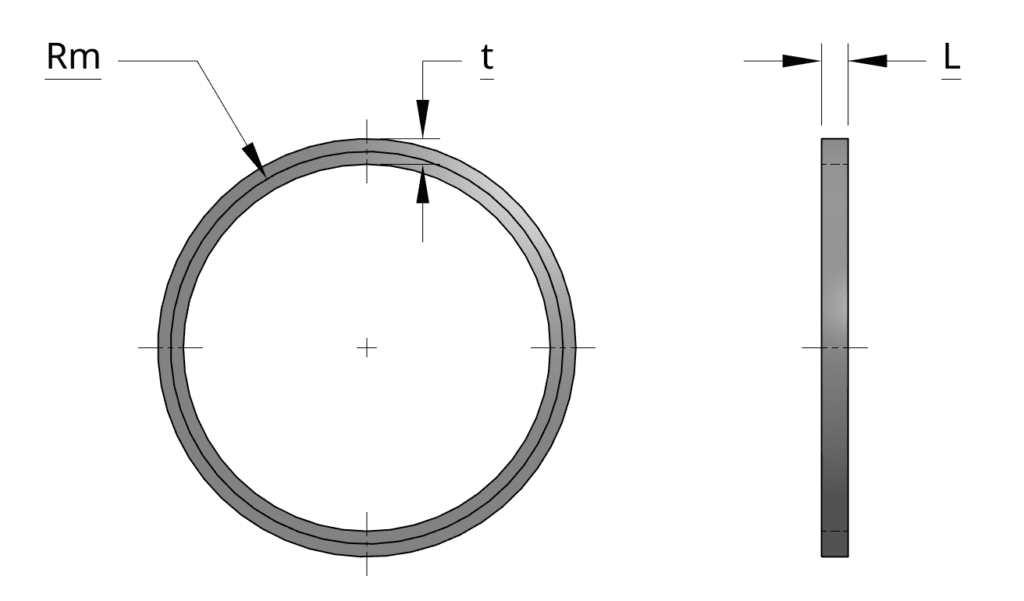
    geometry model parameters for frequency analysis of a ring validation case
    Figure 1: Geometry model and parameters

    The ring has a length \(L\) of 0.05 \(m\), a thickness \(t\) of 0.048 \(m\), and a medium radius \(Rm\) of 0.369 \(m\).

    Analysis Type and Mesh

    Tool Type: Code_Aster

    Analysis Type: Frequency Analysis

    Mesh and Element Types:

    First and second order meshes were computed using the SimScale standard mesh algorithm:

    CaseMesh TypeNumber of
    Nodes    		Element Type
    A1st Order Tetrahedral24755Standard
    B1st Order Tetrahedral24755Standard
    C1st Order Tetrahedral24755Standard
    D2nd Order Tetrahedral172165Standard
    E2nd Order Tetrahedral172165Standard
    F2nd Order Tetrahedral172165Standard
    Table 1: Mesh refinement per case

    A mesh independence study was also performed for the second order meshes and IRAM – Sorensen algorithm to ensure the optimal fineness parameter level.

    Mesh
    #    		Mesh
    Type    		Number of
    Nodes    		Mesh
    Fineness
    12nd Order Tetrahedral6772
    22nd Order Tetrahedral14434
    32nd Order Tetrahedral35576
    42nd Order Tetrahedral140048
    Table 2: Mesh convergence study details
    tetrahedral finite elements mesh for frequency analysis of a ring validation case
    Figure 2: Tetrahedral finite element mesh used for all cases

    Simulation Setup

    Material:

    • Linear Elastic Isotropic:
      • \( E = \) 185 \(GPa \)
      • \( \nu = \) 0.3
      • \( \rho = \) 7800 \(kg.m^{-3} \)

    Boundary Conditions:

    • Constraints:
      • Body is free in space.

    Computing Algorithm:

    The following available computing algorithms were compared in the different cases:

    CaseNatural Frequencies
    Computing Algorithm
    AIRAM – Sorensen
    BLanczos
    CBathe – Wilson
    DIRAM – Sorensen
    ELanczos
    FBathe – Wilson
    Table 3: Computing algorithms by case

    The main characteristics of each algorithm are summarized below [U4.52.02]\(^2\):

    • IRAM – Sorensen: Uses a sub-space decomposition method to compute the natural frequencies and modes. Suitable for real and complex, symmetrical or non-symmetrical matrices.
    • Lanczos: Uses a sub-space decomposition method to compute the natural frequencies and modes. Suitable for real, symmetrical only matrices.
    • Bathe – Wilson: Uses a sub-space decomposition method to compute the natural frequencies and modes. Suitable for real, symmetrical only matrices.

    A fourth algorithm is also available in SimScale, called QZ. This algorithm suffers from high memory consumption, which limits its application to cases with less than 1000 degrees of freedom. Therefore, it is not suitable for the current validation case.

    Note

    Complex matrices appear in the frequency analysis of materials with frequency damping. As this model is not available in SimScale, the difference between the algorithms comes down to robustness and speed.

    Frequency Reference Solution

    The reference solution is of numerical type, as developed in [SDLS109]\(^1\). The solution is presented in terms of all the natural frequencies and their corresponding shapes in the frequency range [200, 800] \(Hz\). This solution was achieved by a convergence analysis using hexahedral elements, and as reported in the reference, a precision of 5% of the computed frequencies is estimated.

    The consulted reference solution is:

    ModeNatural Frequency \([Hz]\)
    Ovalization210.55
    210.55
    Trifoliate587.92
    587.92
    Out of Plane205.89
    205.89
    588.88
    588.88
    Table 4: Reference solution for different frequency modes

    Frequency Results Comparison

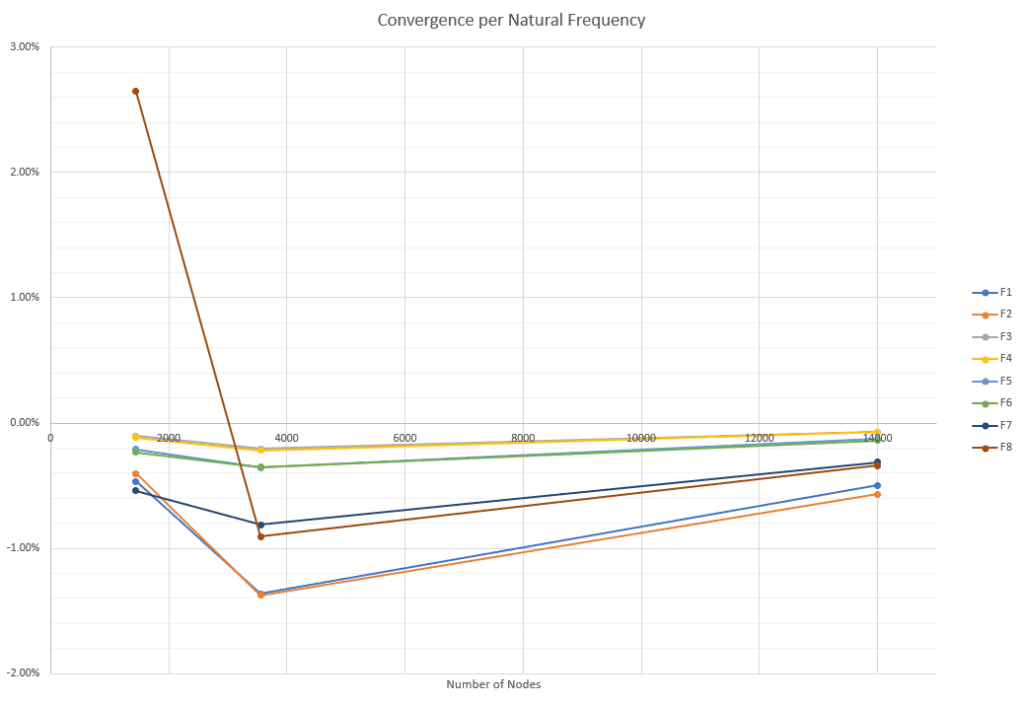
    Below can be found the results of the mesh independence study. For each natural frequency (F1 through F8), the variation of the result (in percent) with respect to the previous solution is plotted against the number of nodes in the mesh. At the final, finer mesh, the solution precision is 0.6% or lower.

    mesh convergence analysis plot for frequency analysis of a ring validation case
    Figure 3: Mesh convergence analysis results for second order mesh.
    Here, F1 means first frequency, F2 second frequency, and so on.

    Comparison of computed natural frequencies with the reference solution for each case can be seen below:

    ModeReference SolutionSimScale SolutionError
    Ovalization210.55213.3321.32 %
    210.55213.9661.62 %
    Trifoliate587.92596.3431.43 %
    587.92596.6981.49 %
    Out of Plane205.89210.0172.00 %
    205.89210.2442.11 %
    588.88599.5121.81 %
    588.88599.5211.81 %
    Table 5: Case A results
    ModeReference SolutionSimScale SolutionError
    Ovalization210.55215.1812.20 %
    210.55216.092.63 %
    Trifoliate587.92601.832.37 %
    587.92602.3162.45 %
    Out of Plane205.89212.8223.37 %
    205.89213.0983.50 %
    588.88606.6853.02 %
    588.88606.7943.04 %
    Table 6: Case B results
    ModeReference SolutionSimScale SolutionError
    Ovalization210.55215.1812.20 %
    210.55216.092.63 %
    Trifoliate587.92601.832.37 %
    587.92602.3162.45 %
    Out of Plane205.89212.8223.37 %
    205.89213.0983.50 %
    588.88606.6853.02 %
    588.88606.7943.04 %
    Table 7: Case C results
    ModeReference SolutionSimScale SolutionError
    Ovalization210.55209.998-0.26 %
    210.55209.998-0.26 %
    Trifoliate587.92586.293-0.28 %
    587.92586.293-0.28 %
    Out of Plane205.89205.143-0.36 %
    205.89205.144-0.36 %
    588.88586.975-0.32 %
    588.88586.975-0.32 %
    Table 8: Case D results
    ModeReference SolutionSimScale SolutionError
    Ovalization210.55209.998-0.26 %
    210.55209.998-0.26 %
    Trifoliate587.92586.293-0.28 %
    587.92586.293-0.28 %
    Out of Plane205.89205.143-0.36 %
    205.89205.144-0.36 %
    588.88586.975-0.32 %
    588.88586.975-0.32 %
    Table 9: Case E results
    ModeReference SolutionSimScale SolutionError
    Ovalization210.55209.998-0.26 %
    210.55209.998-0.26 %
    Trifoliate587.92586.293-0.28 %
    587.92586.293-0.28 %
    Out of Plane205.89205.143-0.36 %
    205.89205.144-0.36 %
    588.88586.975-0.32 %
    588.88586.975-0.32 %
    Table 10: Case F results

    Results are mesh dependent instead of algorithm dependent because all algorithms produce similar results. The difference between algorithms can be seen when looking at the running times. Cases using IRAM – Sorensen and Lanczos algorithm are much faster than Bathe – Wilson. The recommendation is then to stay with the default algorithm (IRAM – Sorensen), because of its known robustness.

    AlgorithmRuntime
    1st Order Mesh    		Runtime
    2nd Order Mesh
    IRAM – Sorensen2 min13 min
    Lanczos2 min13 min
    Bathe – Wilson9 min139 min
    Table 11: Comparison of runtime for each algorithm

    Following are the referenced natural mode shapes as seen on the online post-processor:

    natural vibration shapes plot for frequency analysis of a ring validation case
    Figure 4: Natural vibration shapes for each natural frequency taken from case D.

    References

    • SDLS109 – Fréquences propres d’un anneau cylindrique épais – Code_Aster validation case
    • [U4.52.02] – Opérateur CALC_MODES – Code_Aster utilization manual

    Note

    If you still encounter problems validating you simulation, then please post the issue on our forum or contact us.

    Last updated: June 30th, 2020

    Contents