websights

Fill out the form to download

Required field
Required field
Not a valid email address
Required field
Required field

  • Set up your own cloud-native simulation in minutes.

    • Documentation

    SimScale DocumentationValidation CasesValidation Case: Cantilever Plate Subjected to a Follower Pressure

    Validation Case: Cantilever Plate Subjected to a Follower Pressure

    This validation case belongs to solid mechanics. It uses a cantilever plate geometry to validate the follower pressure boundary condition.

    SimScale results are compared to simulation results, presented in [SSNV145]\(^1\). The reference uses Code_Aster to perform the analysis.

    View Project

    Geometry

    The geometry for this project consists of a cantilever plate, as seen in Figure 1:

    cantilever plate follower pressure validation case
    Figure 1: Cantilever plate geometry. The results will be assessed at point P.

    The dimensions of the geometry are given in Table 1:

    CoordinatesABCDEFGHP
    x \([m]\)00001010101010
    y \([m]\)0.5-0.5-0.50.50.5-0.5-0.50.50
    z \([m]\)-0.05-0.050.050.05-0.05-0.050.050.050
    Table 1: Coordinates of points within the cantilever plate geometry

    Analysis Type and Mesh

    Tool Type: Code_Aster

    Analysis Type: Nonlinear static

    Mesh and Element Types: Two meshes are used in this case. The first one is a second-order mesh created in SimScale with the standard algorithm. Case B uses a second-order hexahedral mesh. It was created locally and imported to SimScale.

    Table 2 contains details of the resulting meshes:

    CaseMesh TypeNodesElement Type
    ASecond-order standard9700Standard
    BSecond-order hexahedral3502Standard
    Table 2: Characteristics of the meshes used for cases A and B

    Figure 2 shows the standard mesh, used for case A:

    second order standard mesh cantilever beam
    Figure 2: Discretization obtained with a second-order standard mesh

    Similarly, Figure 3 shows the second-order hexahedral mesh, that was imported to SimScale.

    hexahedral mesh imported to simscale med
    Figure 3: Hexahedral mesh imported to SimScale. It contains a total of 3502 nodes.

    Note

    Especially for nonlinear analysis, such as this one, we recommend second-order meshes. They provide more accurate results, due to the higher number of nodes.

    The following article provides further information on second-order meshes for finite element analysis.

    Simulation Setup

    Material:

    • Material behavior: Linear elastic
    • \((E)\) Young’s modulus = 1.2e+7 \(Pa\)
    • \((\nu)\) Poisson’s ratio = 0.3
    • \((\rho)\) Density = 1000 \(kg/m³\)

    Boundary Conditions:

    The boundary conditions will be defined based on Figure 1:

    • Constraints
      • Fixed support on face ABCD
    • Surface loads
      • Follower Pressure \(P\), applied on face CDHG. The following formulation is used:
        $$P = t \tag{1}$$
        Where \(t\) is the pseudo-time for the nonlinear analysis. This validation case will run until \(t\) = 26.

    Result Comparison

    SimScale results will be compared against two reference simulations. The first one used Code_Aster, while the remaining one used the SAMCEF software.

    The results for both reference simulations are found in [1]. The displacements in the X and Z-directions are evaluated at point P (as seen in Figure 1).

    In Figure 4, we compare the results for the displacements in the X-direction against Code_Aster. The reference results were extracted using WebPlotDigitizer.

    follower pressure validation case displacement results
    Figure 4: Result comparison between SimScale results and the reference simulation for DX

    A similar comparison was made for the displacements in the Z-direction:

    follower pressure validation case displacement results vertical direction
    Figure 5: Result comparison between SimScale results and the reference simulation for DZ

    Additionally, still using point P as a reference, the displacements obtained with SimScale are compared to the results from the SAMCEF software\(^1\). Table 1 contains the displacements in the X-direction:

    Pseudo-time \([s]\)SAMCEF – DX \([m]\)Case A – DX \([m]\)Error [%]Case B – DX \([m]\)Error [%]
    11-7.3664-7.0953-3.68-7.0725-3.99
    13-9.03743-8.7143-3.58-8.6851-3.90
    22-13.5098-13.2380-2.01-13.2049-2.26
    26-14.1513-13.9797-1.21-13.9555-1.38
    Table 3: Comparison between SimScale and SAMCEF results, for the displacements in the X-direction

    A comparison for the displacements in the Z-direction is also presented:

    Pseudo-time \([s]\)SAMCEF – DZ \([m]\)Case A – DZ \([m]\)Error [%]Case B – DZ \([m]\)Error [%]
    11-8.44920-8.3929-0.67-8.3872-0.73
    13-8.42753-8.43100.04-8.42990.02
    22-5.78828-6.07594.97-6.10575.48
    26-4.43375-4.76967.57-4.80798.44
    Table 4: Comparison between SimScale and SAMCEF results, for the displacements in the Z-direction

    The results obtained with SimScale for both directions show a great agreement with the reference simulations.

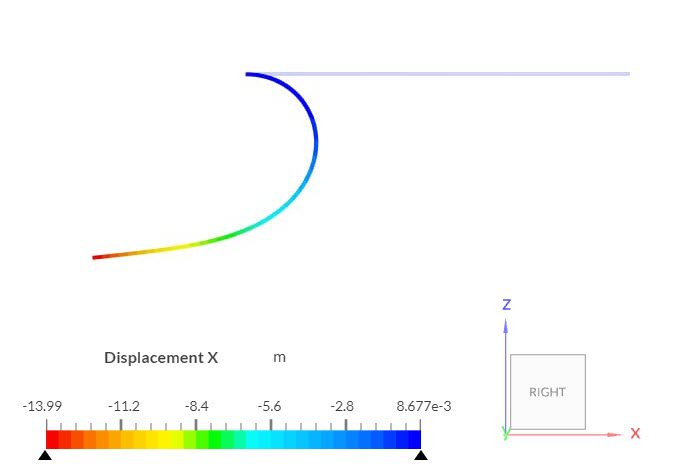
    Figure 6 shows the contours for displacements in the X-direction, for case A. The follower pressure boundary condition is updated after each pseudo time step, based on the current deformed state of the geometry. As a result, the plate gets rolled up:

    follower pressure displacement contours
    Figure 6: Displacement contours in the X-direction for case A. The initial position of the plate is shaded in blue.

    References

    Last updated: September 4th, 2023

    Contents