Validation Case: Bimetallic Strip Under Thermal Load

This validation case belongs to thermomechanics, with the case of a bimetallic strip under thermal load. The aim of this test case is to validate the following parameters:

Thermomechanical solver
Multiple materials and bonded contact

The simulation results of SimScale were compared to theoretical computations derived from [Roark’s] $^{1}$ .

View Project

Geometry

The geometry used for the case is as follows:

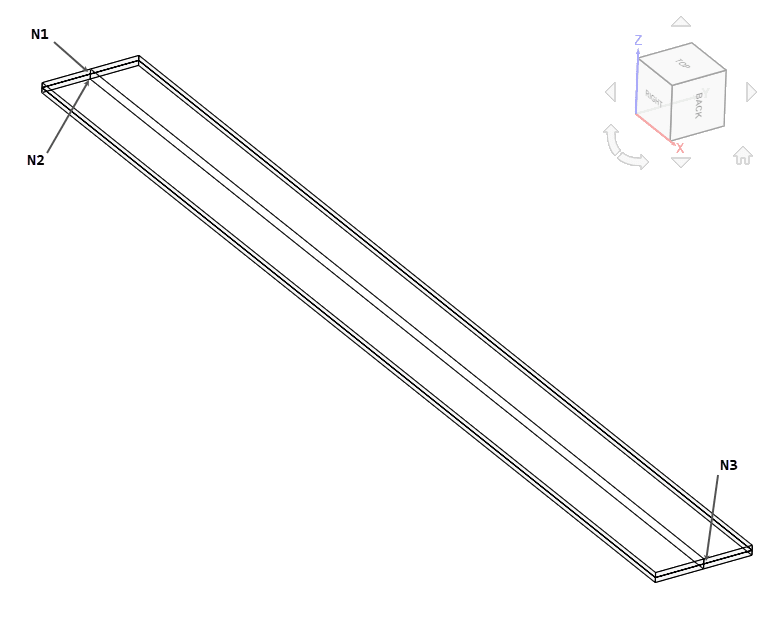
It represents a strip with length $l$ of 10 $m$ , width $w$ of 1 $m$ and thickness $t$ of 0.1 $m$ , composed of two strips each with thickness $t_{a}, t_{b}$ of 0.05 $m$ . Nodes N1 and N3 are located at mid-thickness and node N2 is located at the bottom surface as shown in figure 1.

Analysis Type and Mesh

Tool Type: Code_Aster

Analysis Type: Thermomechanical steady state with static inertia effect

Mesh and Element Types:

Mesh Type	Number of Nodes	Element Type
2nd order hexahedral	3652	Standard

Table 1: Mesh details

The hexahedral mesh was computed locally and uploaded into the simulation project.

hexahedral mesh bimetallic strip thermomechanical validation case — Figure 2: Finite elements hexahedral mesh used for the simulation (closer view on the left)

Simulation Setup

Material:

Top Strip:
- Elastic Modulus $E_{a} =$ 200 $G P a$
- Poison’s ratio $ν_{a} =$ 0
- Density $ρ_{a} =$ 7870 $k g / m^{3}$
- Thermal conductivity $κ_{a} =$ 60 $W / (m K)$
- Expansion ratio $γ_{a} =$ 1e-5 $1 / K$
- Reference temperature 300 $K$
- Specific heat $C_{p a} =$ 480 $J / (k g K)$
Bottom Strip:
- Elastic Modulus $E_{b} =$ 200 $G P a$
- Poison’s ratio $ν_{b} =$ 0
- Density $ρ_{b} =$ 7870 $k g / m^{3}$
- Thermal conductivity $κ_{b} =$ 60 $W / (m K)$
- Expansion ratio $γ_{b} =$ 2e-5 $1 / K$
- Reference temperature 300 $K$
- Specific heat $C_{p b} =$ 480 $J / (k g K)$

Boundary Conditions:

Constraints:
- N1 restrained with $d_{x} = d_{y} = d_{z} =$ 0 $m$
- N2 restrained with $d_{x} = d_{y} =$ 0 $m$
- N3 restrained with $d_{y} =$ 0 $m$
- Fixed temperature $T =$ 400 $K$ applied on top and bottom surfaces
Contacts:
- Bonded contact between the strips

Reference Solution

The reference solution is of the analytical type, as presented in [Roark’s] $^{1}$ . It is given in terms of the displacements of the free end of the strip and the stress at the bottom surface:

$d_{x} = l (T - T_{0}) \frac{γ_{a} + γ_{b}}{2}$

$d_{z} = \frac{3 l^{2} (γ_{b} - γ_{a}) (T - T_{0}) (t_{a} + t_{b})}{t_{b}^{2} K_{1}}$

$σ_{b o t t o m} = \frac{(γ_{b} - γ_{a}) (T - T_{0}) E_{b}}{K_{1}} [3 \frac{t_{a}}{t_{b}} + 2 - \frac{E_{a}}{E_{b}} (\frac{t_{a}}{t_{b}})^{3}]$

$K_{1} = 4 + 6 \frac{t_{a}}{t_{b}} + 4 (\frac{t_{a}}{t_{b}})^{2} + \frac{E_{a}}{E_{b}} (\frac{t_{a}}{t_{b}})^{3} + \frac{E_{b}}{E_{a}} \frac{t_{b}}{t_{a}}$

The computed solutions are:

$d_{x} = 0.015 m$

$d_{z} = 0.75 m$

$σ_{b o t t o m} = 50 M P a$

Result Comparison

A comparison of displacements at point N3 and stress $σ_{X X}$ at point N2 with theoretical solution is presented below:

POINT	FIELD	COMPUTED	REF	ERROR
N3	DX $[m]$	0.015	0.015	0.00 %
N3	DZ $[m]$	0.7479	0.75	-0.28 %
N2	SIXX $[M P a]$	48.7631	50	-2.47 %

Table 2: Results comparison and computed errors

Illustration of the deformed shape and stress distribution on the bimetallic strip below:

stress contours developed due to deformation in simscale postprocessor thermomechanical — Figure 3: Deformed shape and stress contour on the bimetallic strip

Advanced Tutorial: Thermomechanical Analysis of an Engine Piston

References

(2011)”Roark’s Formulas For Stress And Strain, Eighth Edition”, W. C. Young, R. G. Budynas, A. M. Sadegh

Note

If you still encounter problems validating you simulation, then please post the issue on our forum or contact us.

Last updated: May 19th, 2021

Did this article solve your issue?

How can we do better?

We appreciate and value your feedback.