Validation Case: 3D Punch With Rounded Edges (NAFEMS Contact Benchmark 2)

This 3D punch contact validation case belongs to solid mechanics. This test case aims to validate the following parameters:

Penalty contact
Friction

The simulation results of SimScale were compared to the analytical results derived from [NAFEMS_R94]\(^1\).

View Project

Geometry

The geometry consists of a punch (DGHIJK) on top of a foundation (ABCDEF). The 3D punch has a 10 \(mm\) radius fillet at the edge of the contact with the foundation. Figure 1 shows a wireframe of the geometry:

Due to the symmetry of the problem, only a quarter of the model is used for the simulations. These are the coordinates for each of the points:

	A	B	C	D	E	F	G	H	I	J	K
x \([mm]\)	0	0	0.1	0	0	0.1	0	0.04	0	0	0.05
y \([mm]\)	-0.2	-0.2	-0.2	0	0	0	0	0	0.1	0.1	0.1
z \([mm]\)	0	0.1	0	0	0.1	0	0.4	0	0	0.5	0

Table 1: Coordinates of points A through K in the CAD model

The following dimensions are used in the creation of the geometry:

Geometry Feature	Dimension \([mm]\)
Punch diameter	100
Punch height	100
Foundation diameter	200
Foundation height	200
Fillet radius at the edge of the punch contact	10

Table 2: Punch and foundation dimensions, in meters

Analysis Type and Mesh

Tool Type: Code_Aster

Analysis Type: Dynamic

Mesh and Element Types: The meshes used in this project were created in SimScale with the standard algorithm.

Case	Element Type	Nodes	Element Technology	Solution Method	Contact Smoothing	Penalty Coefficient	Coefficient of Friction
A	1st Order Tetrahedral	32101	Standard	Penalty	On	1e14	0
B	2nd Order Tetrahedral	50226	Reduced Integration	Penalty	On	1e14	0
C	1st Order Tetrahedral	32101	Standard	Penalty	On	1e14	0.1
D	2nd Order Tetrahedral	50226	Reduced Integration	Penalty	On	1e14	0.1

Table 3: Mesh characteristics and contact settings for cases A through D

Find below the mesh used for cases B and D. It’s a standard mesh with second-order tetrahedral cells.

second order standard mesh for validation — Figure 2: Second-order standard mesh used for cases B and D

Simulation Setup

Material:

3D Punch
- Material behavior: Linear elastic
- \(E\) = 210 \(GPa\)
- \(\nu\) = 0.3
- \(\rho\) = 7870 \(kg/m³\)
Foundation
- Material behavior: Linear elastic
- \(E\) = 70 \(GPa\)
- \(\nu\) = 0.3
- \(\rho\) = 7870 \(kg/m³\)

Boundary Conditions:

Constraints
- \(d_x\) = 0 on faces ABED and DGJI;
- \(d_z\) = 0 on faces ACFD and DHKI;
- Fixed support on face ABC.
Surface loads
- Pressure = \(10^8 \ Pa\) on face IJK.

Result Comparison

Comparison of the displacements and the normal pressure of the nodes on edge DE. The values of reference in all figures were calculated with MSC.MARC and extracted from [NAFEMS_R94]\(^1\) with WebPlotDigitizer.

The first plot is a comparison between the axial displacements from the cases without friction and the reference values:

axial displacements 3d punch no friction — Figure 3: Axial displacements on the DE edge, showing good agreement with reference values

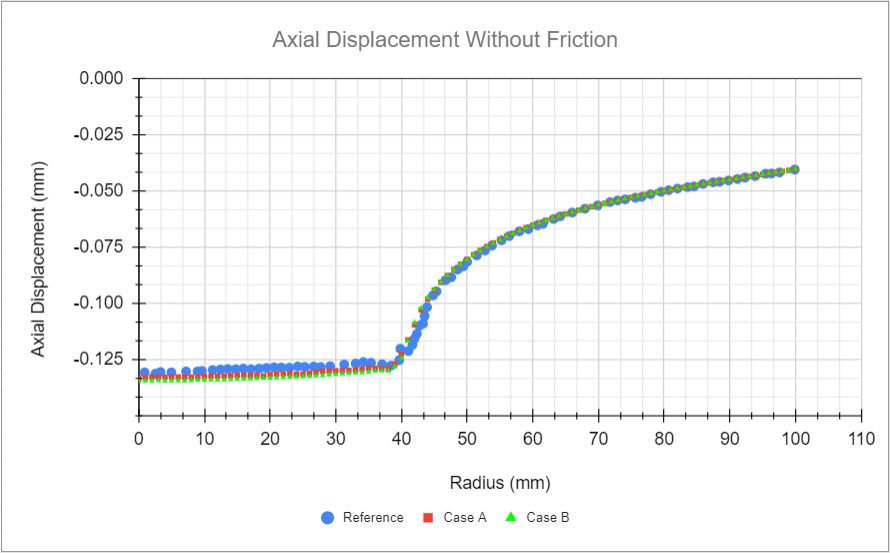
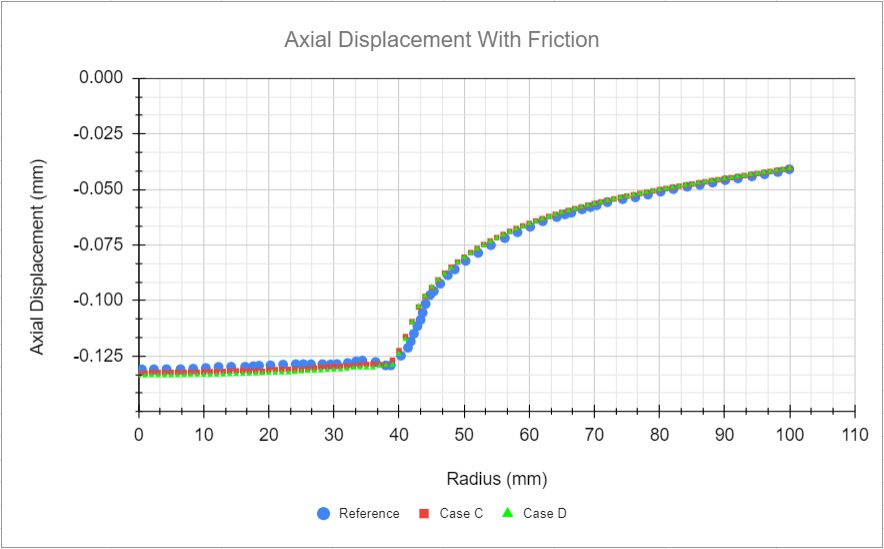
Now, comparing axial displacement from the cases with the friction and the reference values. Similarly to the previous case, a very good agreement is observed here:

axial displacements 3d punch with friction — Figure 4: Axial displacements on the DE edge, with friction being modeled

Now, still analyzing the results over the DE edge, we will compare the radial displacements obtained with SimScale to the reference ones.

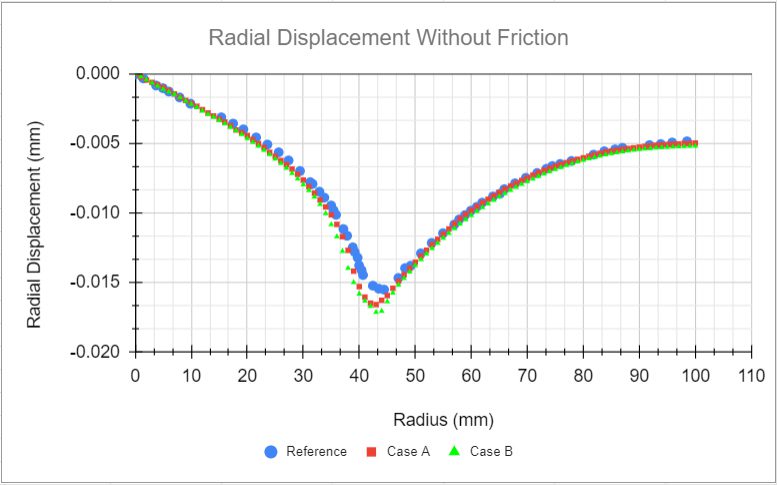
radial displacements 3d punch no friction — Figure 5: Radial displacements on the DE edge, for the cases with no friction

Figure 6 shows contours for \(y\) displacement, in meters, for case D:

y displacement contours on a punch on a cylinder case in simscale post processor — Figure 6: Contours for the displacements observed in the y-direction

References

Last updated: September 30th, 2021

Did this article solve your issue?

How can we do better?

We appreciate and value your feedback.