Advanced Tutorial: Smoke Propagation From a Chimney

This article provides a step-by-step tutorial for smoke propagation in the open air, making use of the passive scalar transport formulation.

passive scalar analysis of a power plant with streamlines — Figure 1: Smoke propagating off the chimneys of a power plant

Overview

This smoke propagation simulation tutorial teaches how to:

Set up and run a convective heat transfer simulation with passive species;
Assign boundary conditions, material, and other properties to the simulation;
Set up walls with a given wall roughness;
Define an Atmospheric Boundary Layer (ABL) profile for the inlet;
Mesh with the SimScale standard meshing algorithm;

We are following the typical SimScale workflow:

Preparing the CAD model for the simulation.
Setting up the simulation.
Creating the mesh.
Run the simulation and analyze the results.

1. Prepare the CAD Model and Select the Analysis Type

First of all click, the button below. It will copy the smoke propagation project containing the geometry into your workbench.

Import tutorial into Workbench

The following picture shows how the workbench looks after importing the project.

smoke propagation initial geometry — Figure 2: Workbench after importing the tutorial project

In this example, we want to have multiple faces on the ground to assign different terrain roughness. Therefore, we modeled the air domain in CAD software and split the ground surface.

Did you know?

For simulations involving external flow, it’s important that the flow region is large. This is mostly necessary to avoid interferences from the boundaries. Furthermore, the domain should be longer downstream from the geometry, to capture the wake effects.

Assuming “L” is the longest edge of any building in the geometry, use the following rule of thumb to create a flow domain.

enclosure external aerodynamics size — Figure 3: Minimum enclosure size. The enclosure should be longer in the downstream direction.

1.2 Create the Simulation

To set up a new simulation, select the geometry in the left-hand side panel:

creating a new simulation — Figure 4: Creating a simulation for the geometry

Hitting the ‘Create simulation’ button leads to the following options:

creating a convective heat transfer simulation — Figure 5: Analysis types available in SimScale.

Choose ‘Convective heat transfer’ for analysis type and ‘Create the simulation’.

Now you can see the default simulation tree presented in the following picture:

adding passive species to convective heat transfer — Figure 6: Global settings for the convective heat transfer simulation.

In the global simulation setup, please change the Turbulence model to ‘k-omega SST’. This model switches in between k-omega and k-epsilon automatically, therefore it takes advantage of both models.

Also, add 2 Passive species. These will help to define the sources of smoke from the chimneys and differentiate the concentration of them and clean air.

2. Set up the Simulation

In this part of the tutorial, we will define the physics of the model we want the solver to calculate.

2.1 Define a Material

This simulation will use ‘Air’ as fluid material. Therefore click on the ‘+ button’ next to Materials. In doing so, a library of fluid materials opens:

choosing a material to the parts — Figure 7: Fluid materials library.

Select ‘Air’ and click ‘Apply’. In the window that opens, you can leave the default values and assign them to the entire flow region.

2.2 Model

In the next step, we define gravity according to the global coordinate system. Therefore click on Model in the simulation tree.
For this geometry, the gravity direction is in the negative z-axis. Hence, input ‘-9.81’ in the z-direction. Leave the Diffusion coefficients and Turbulent Schmidt number as default.

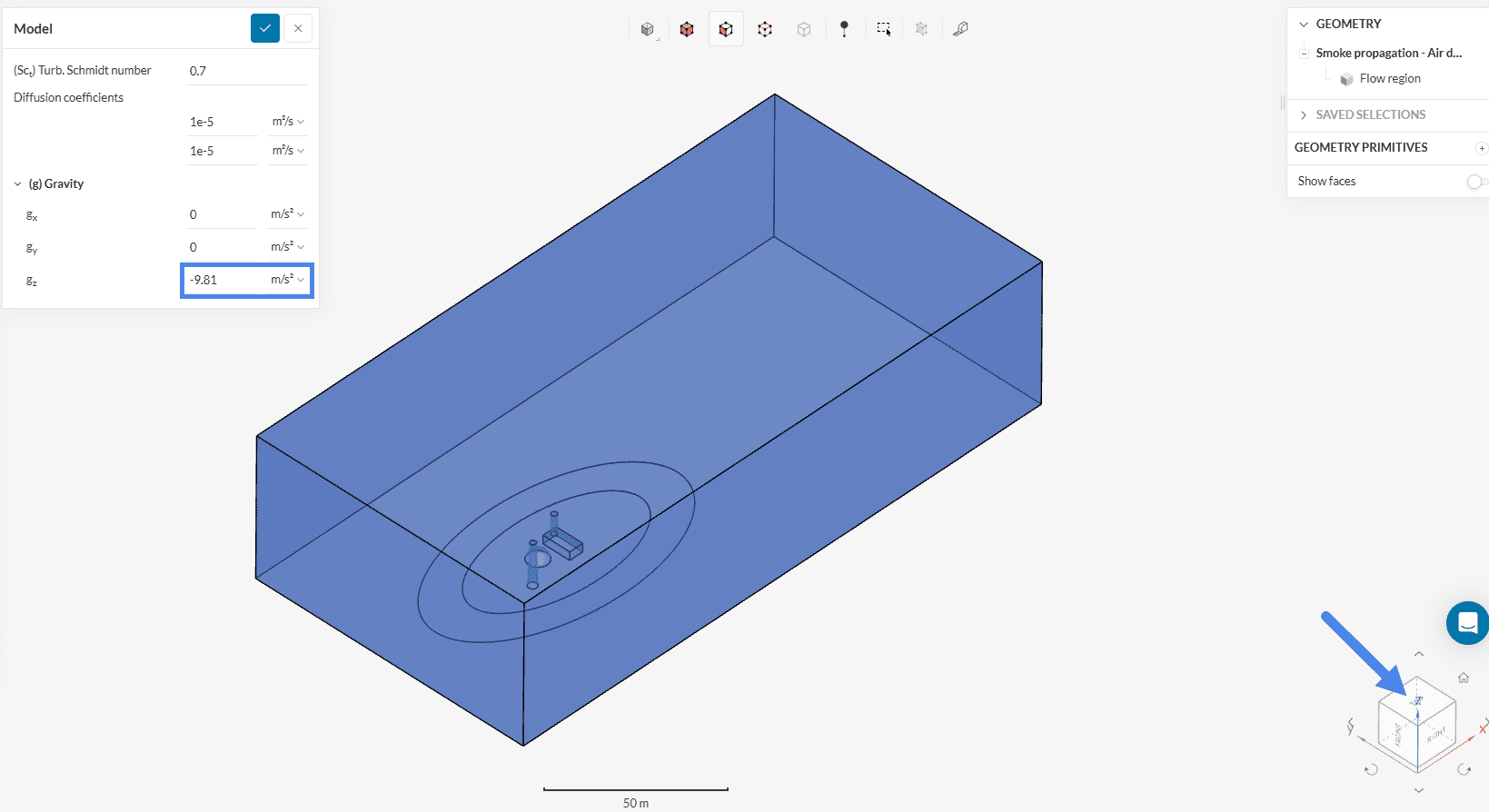
gravity set up cfd simulations — Figure 9: Configuring gravity in the model tab. The direction is based on the orientation cube in the bottom right corner.

2.2 Assign the Boundary Conditions

The following picture summarizes the boundary conditions applied in this simulation:

boundary conditions pollutant dispersion simulation — Figure 9: Overview of the boundary conditions for this tutorial.

a. Walls – Slip

Follow the instructions presented in the picture below to add a new boundary condition:

creating a boundary condition — Figure 10: From the list of boundary conditions, choose ‘wall’.

After hitting the ‘+ button’ next to boundary conditions, a drop-down menu will appear, where one can choose between different boundary conditions;
Select the ‘Wall’ boundary condition.

slip wall external aerodynamics — Figure 11: Assigning a slip wall condition to the top and sides of the enclosure.

Change (U) velocity to ‘Slip’ and (T) Temperature to ‘Adiabatic’. Now assign the top, left, and right walls to this condition.

b. Pressure Outlet

Create a new boundary condition, but this time choose ‘Pressure outlet’. The outlet is further away from the chimneys.

setting up a pressure outlet boundary condition wind tunnel — Figure 12: Pressure outlet boundary condition.

c. Velocity Inlet – Chimneys

Create yet another boundary condition. Select ‘Velocity inlet’. Let’s first set up the inlet for the tall chimney.

passive scalar transport inlet — Figure 13: Setting up a velocity inlet with passive scalars.

Smoke will be released at ‘8 $m/s$’ in the z direction (Uz) and at
A (T) Temperature of ‘450 $°C$’.
The first passive species is therefore linked to the inlet flow from the tall chimney. That is why we select ‘1’ for the first Value within Passive scalars.

Set up another velocity inlet, this time for the short chimney:

velocity inlet with passive species — Figure 14: Velocity inlet for the short chimney. This one is linked to the second passive species.

Velocity will be ‘5 $m/s$’ in the positive z-direction.
The temperature is ‘300 $°C$’.
This inlet will receive a Value of ‘1’ for the second passive species.

d. Velocity Inlet – ABL

In this step, we will set up an Atmospheric Boundary Layer (ABL). It consists of a pre-defined velocity profile, with a value zero on the ground, gradually increasing with height. In this tutorial, $u_{ref}$ is 5 $m/s$ and $h_{ref}$ is 10 $m$.

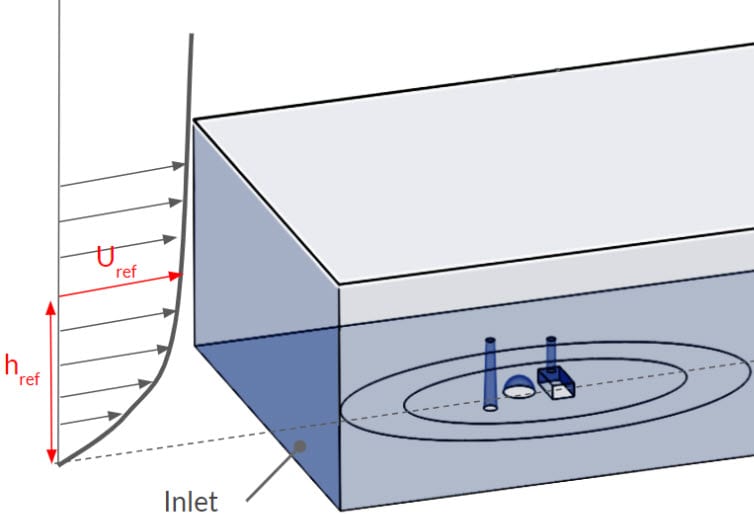
atmospheric boundary layer set up cfd — Figure 15: Atmospheric boundary layer showing the velocity profile at the inlet.

Refer to these equations for the formulation of the logarithmic profile:

This logarithmic profile has the following formulation:

$$u = \frac{u^{*}}{K} \cdot ln \left (\frac{z + z_{0}}{z_{0}} \right ) \tag{1}$$

Where

‘K‘ is the von Karman constant, equal to 0.41;
‘z₀‘ is the aerodynamic roughness length. In this tutorial, we will consider it 0.03 meters;
‘z‘ is the height in which the velocity is calculated;
‘u^*‘ is the friction velocity, given by:

$$u^{*} = K \cdot \frac{u_{ref}} {ln \left (\frac{z_{ref} + z_{0}} {z_{0}} \right )} \tag{2}$$

The turbulent kinetic energy (k) formulation is shown below. $c_\mu$ is the turbulent viscosity constant, equal to 0.09:

$$k = \frac{{u^{*}}^{2}} {\sqrt{c_{\mu}}} \tag{3}$$

Finally, for the specific dissipation rate $\omega$, the formula is:

$$\omega = \frac{u^{*}}{K \cdot \sqrt{c_{\mu}}} \cdot \frac{1}{z + z_{0}} \tag{4}$$

For more information about the setup parameters, please visit this page.

We will use formula inputs for $u$, $k$ and $\omega$. Based on the equations above:

$$ u = \frac{5}{log \left (\frac{10 + 0.03}{0.03} \right) } log \left (\frac{z + 0.03}{0.03} \right) \tag{5} $$

$$ k = \left(\frac{0.41*5}{log \left (\frac{10 + 0.03}{0.03} \right)} \right)^2 \frac{1}{\sqrt{0.09}} \tag{6} $$

$$ \omega = \frac{5}{log \left (\frac{10 + 0.03}{0.03} \right)} \frac{1}{\sqrt{0.09}} \frac{1}{z + 0.03} \tag{7} $$

Follow the same procedure as presented in figure 10 but choose a custom boundary condition:

formula input for velocity — Figure 16: Steps to input the formula for a parameter

To input the formula for velocity, select a ‘Fixed value’, and then click on the highlighted button to open further options:

setting up an atmospheric boundary layer for velocity — Figure 17: In this case, the velocity in the x-direction is a function of height.

Afterward, two tabs will be available: Formula and Table. Switch to the formula input, and paste the velocity formula posted above in the x-direction. Hit ‘Apply’ to save.

Repeat the same process for $k$ and $\omega$. The other parameters should be as follows:

Formula for copy paste

Value	Formula
$(U)$ Velocity	(0.415/log((10+0.03)/0.03))/0.41log((z+0.03)/0.03)
$(k)$ Turb. kinetic energy	((0.41*5)/(log((10+0.03)/(0.03)))^2/(0.09)^0.5)
$ (\omega)$ Specific dissipation rate	(0.415/log((10+0.03)/0.03))/(0.41(0.09)^0.5)*1/(z+0.03)

Table 1: Formula for the ABL setup, with specific values for this tutorial.

custom boundary condition for atmospheric boundary layer — Figure 18: Fully set up custom boundary conditions for the inlet. The settings different from default are highlighted.

Pressure type: ‘Zero gradient’;
(T) temperature: ‘Fixed value’ at ‘19.85 $°C$‘;
$\alpha_t$ Turb. thermal diffusivity: ‘Zero gradient‘.
Passive scalars: ‘Fixed value’ at ‘0’.

e. Building Walls

Solid walls will receive a no-slip condition. Furthermore, we can specify a surface roughness for the building walls, as well as for the terrains. For more information about the surface roughness model, check the relevant documentation.

Optional wall settings

The following custom boundary conditions, to define the surface roughness on building walls and the terrains, can be entirely skipped. This means that these surfaces will automatically receive a no-slip condition.

Create a Custom boundary condition.

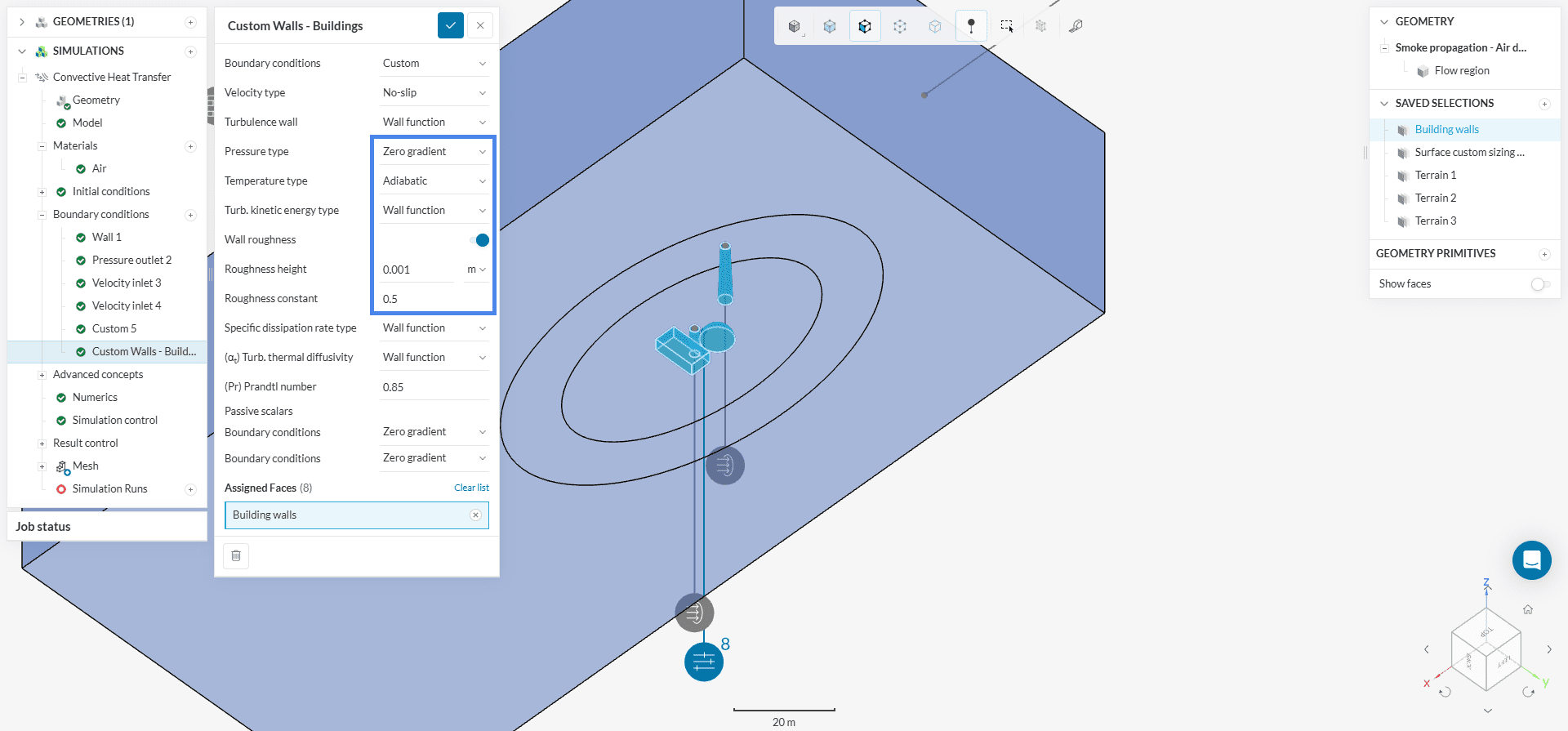
smoke propagation wall roughness setting_building — Figure 19: With this configuration, the building walls receive a uniform wall roughness of 0.001 meters.

Building walls will receive a Roughness height of ‘0.001 $m$’ with a
Roughness constant of ‘0.5’.
To save time, assign this boundary condition to a pre-created saved selection set named ‘Building walls‘:

f. Terrains

The terrains will receive roughness as well. The custom boundary condition is the same as above. The only difference is the Roughness height:

Terrain 1: Roughness height of 0.01 $m$;
Terrain 2: Roughness height of 0.0075 $m$;
Lastly, for terrain 3: Roughness height of 0.005 $m$.

You can also use the pre-saved selection sets to correctly assign the terrains.

smoke propagation wall roughness setting_terrain — Figure 20: Setting up the wall roughness for a terrain.

Repeat the same process for terrain 2 and 3.

Note

Check out this page, if you are interested in other boundary conditions available in SimScale.

2.3 Initial Conditions

To enhance convergence, please initialize the velocity field with ‘5 $m/s$ ‘ in the x-direction. This velocity represents $u_{ref}$:

velocity global settings initial condition — Figure 21: Initializing the global velocity field with the reference wind velocity value.

2.4 Numerics and Simulation Control

The default settings for Numerics are optimized based on the analysis type. Therefore, they work well for most of the simulations and require no changes. However, if you are a simulation expert, you have full control over the settings and may change them as you like.

Access the Simulation control. Here we can define the number of iterations for the simulations as well as the write interval for specifying how many intermediate results to save.

simulation control settings — Figure 22: Adjusting the number of iterations and writing controls for the simulation.

In Simulation control, change the End Time and the Write interval to ‘600’. Furthermore, please adjust the Maximum runtime to 30000 seconds.

Note

For more information about simulation control and numerics, check the corresponding documentation pages.

2.5 Result Control

By setting result controls, you can observe the convergence behavior of several parameters of interest. Hence it is an important indicator to evaluate the quality and trustability of the results.

For this simulation, set up an Area average result control on the outlet. Please proceed as below:

setting result controls to assess convergence — Figure 23: This result control monitors the average levels for all parameters at the outlet.

Expand the Result control tab;
Click on the ‘+ button‘ next to Surface data;
Set Write interval to 5. This should be enough to see the convergence patterns;
Assign it to the outlet face.

3. Mesh

To create the mesh, we recommend using the standard algorithm. This algorithm is a good choice in general, as it is quite automated and delivers good results for most of the geometries.

standard mesh external flow set up — Figure 24: Main settings for the standard algorithm.

Disable Automatic boundary layers. The layers will be specified manually later. To improve the resolution around the areas of interest, we will set up three refinements.

Click on the ‘+ button’ next to Refinements. The first refinement is a Local element size. This refinement limits the maximum edge length of cells in chosen entities. Hence, it’s useful to improve the resolution in specific regions.

local element size refinement in the standard mesher — Figure 25: Local element size refinement applied to a saved selection set.

Click on the ‘+ button’ next to Refinements.
Limit the Element size to 0.3 $m$:
To save time, assign it to a previously created saved selection set named Local element size refinement. This set consists of the solid walls of the buildings and the smoke inlets. you can find it in the geometry panel on the right side of the workbench.

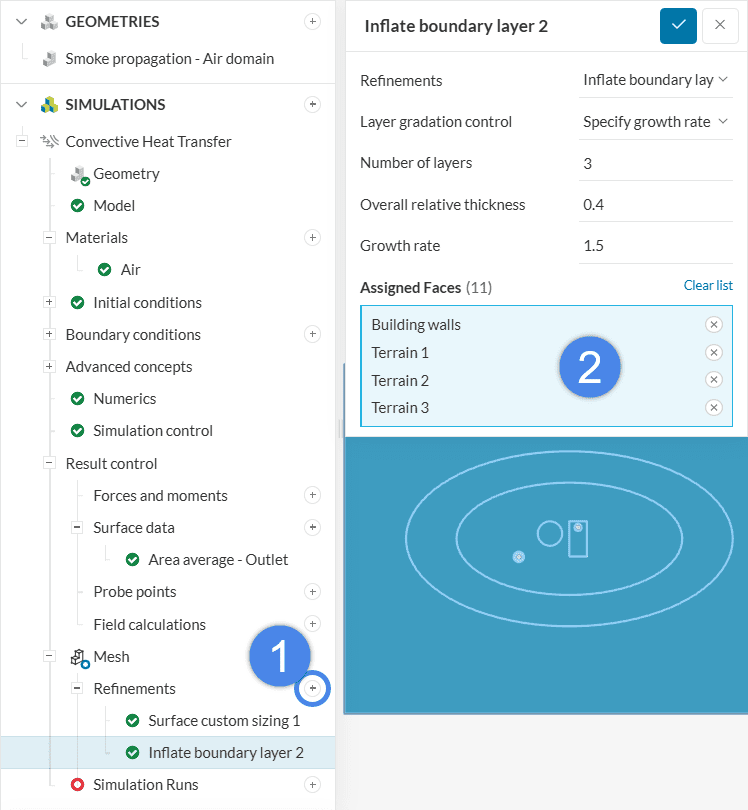
boundary layer refinement standard algorithm — Figure 26: Inflate boundary layer refinement setup. Layers should never be added to inlets and outlets.

Create an Inflate boundary layer refinement.
Keep the settings as default and assign it to these 4 saved selection sets:
- Terrain 1, 2 and 3
- Building Walls

To improve the resolution of the region around the chimneys, let’s create a region refinement. Please proceed as below:

region refinement creation for cfd simulations — Figure 27: Creating a region refinement.

First, create a Region refinement.
Leave 1 meter as Maximum edge length and click on the ‘+ button’ to create a geometry primitive. Choose a Cartesian box and give it the following coordinates:

region refinement to capture wake effects — Figure 28: Cartesian box created for the region refinement. The box should be longer downstream to capture the wake.

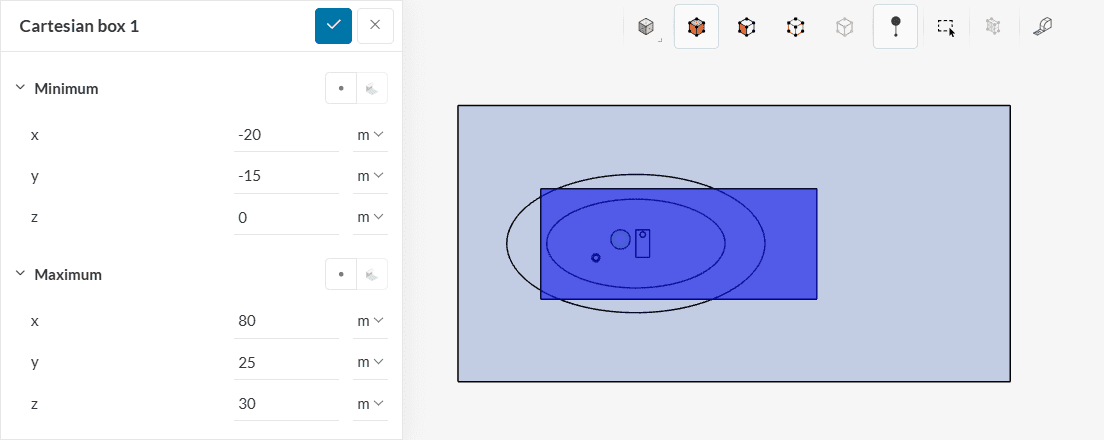
Finally, assign this cartesian box to the region refinement. This step finalizes the setup of the simulation.

4. Start the Smoke Propagation Simulation

Click on the ‘+ button‘ next to Simulation runs and ‘Start‘ the process.

simscale starting a simulation — Figure 29: Starting a new simulation run.

While it’s running, you can access the intermediate results by clicking on Solution fields. They’re updated as the iterations go by!

The entire smoke propagation simulation takes around 100 minutes to finish. In the reference project, which is linked below, we calculated a few more iterations, to assure complete convergence.

accessing post processing environment — Figure 30: To access the post-processing environment, click on either of these two buttons.

5. Post-Processing

5.1 Result Controls

Once the run is finished for your smoke propagation simulation, open the area average at the outlet result control. For steady-state simulations, the parameters are expected to converge and stabilize as iterations go on. Let’s inspect the average level of the first passive scalar (identified as T1):

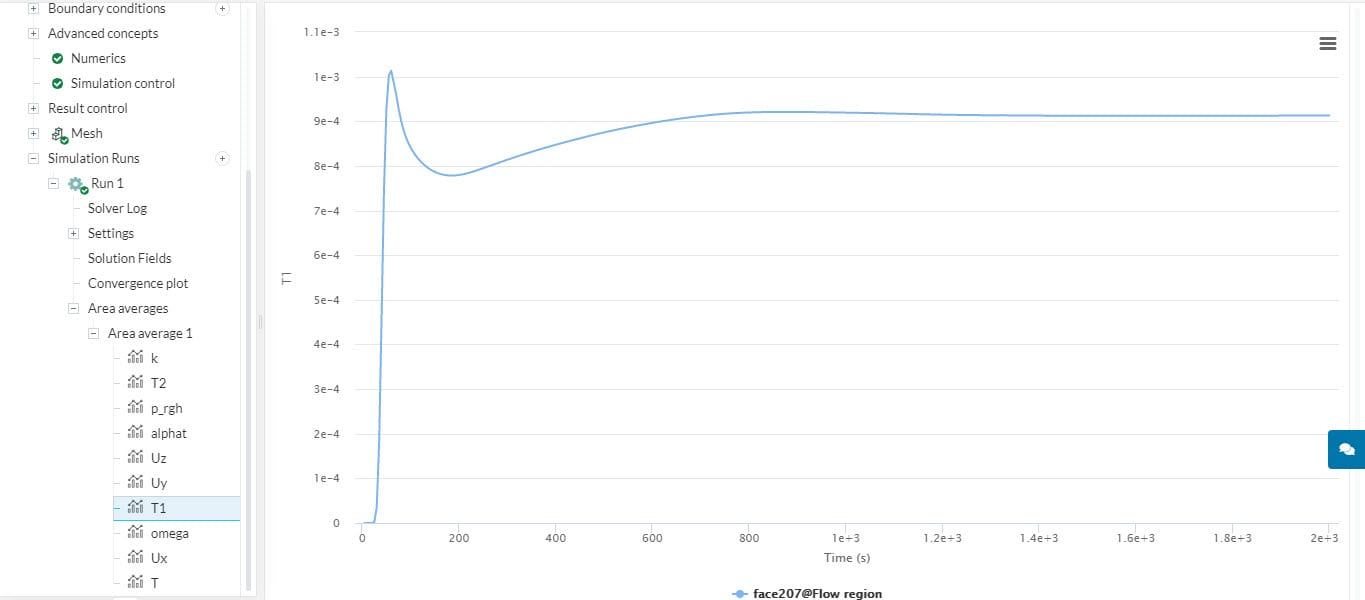
passive scalar result control — Figure 31: Passive scalar level at the outlet, showing good convergence. This is the scalar released by the tall chimney.

For this simulation, other parameters are also useful to assess convergence, such as velocity, temperature, and passive species levels at the outlet.

5.2 Particle Trace

The first post-processor filter that we will use is the ‘Particle Trace’ filter. This filter is very useful to know how the chimneys affect the airflow in the fluid domain. Please follow the steps below to visualize the particle traces:

Toggle off the ‘Cutting Plane’ and create the Particle Traces by selecting the icon in th in the Filters panel and choose ‘Particle Trace’. This will take you to the settings of the particle trace.

smoke propagation 31_Hide Cutting plane and create filter — Figure 32: Toggle off the **‘Cutting Plane’** and choose **‘Particle Trace’** to start to create the particle traces.

Next, place the seeds of the streamlines by clicking on the icon next to Pick Position. Place this at the inlet and align it with the height of the taller chimney. If you want to make sure the height of the seeds is appropriate, you can select the top and side enclosure walls, and hide them by right-clicking and choosing ‘Hide selection’.

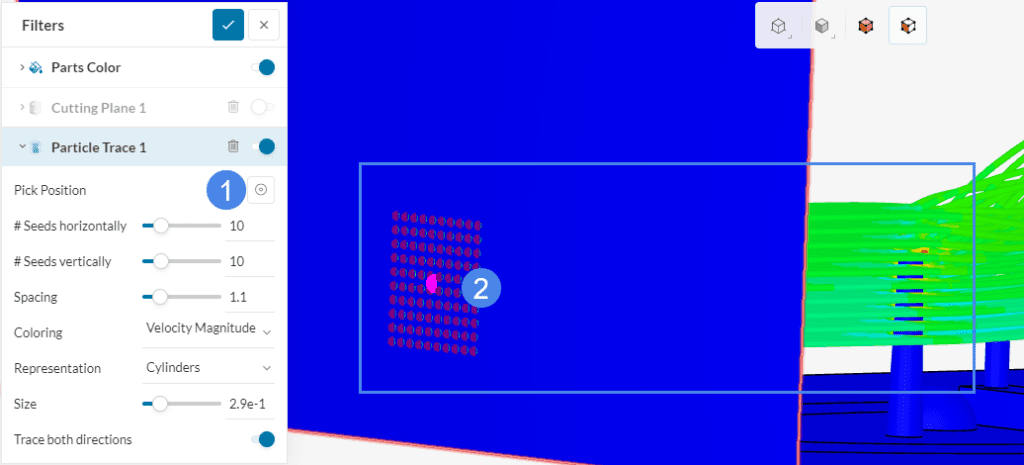
smoke propagation tutorial pick seed point — Figure 33: Click the button beside *Pick Position* to choose the origin point of the particle traces and align it with the height of the chimney.

Adjust the visualization of the streamlines. Increase the number of origin points by changing the #Seeds vertically to ’20’. Reduce the Spacing to ‘0.5’ and Size to ‘0.1’.

Smoke propagation Tutorial particle trace settings — Figure 34: Increase the *#Seeds vertically* to **’20’** and reduce the *Spacing* to **‘0.5’** and *Size* to **‘0.1’**

For the second chimney, you can repeat the same steps outlined above. As a result, the particle traces will be similar to the figure below:

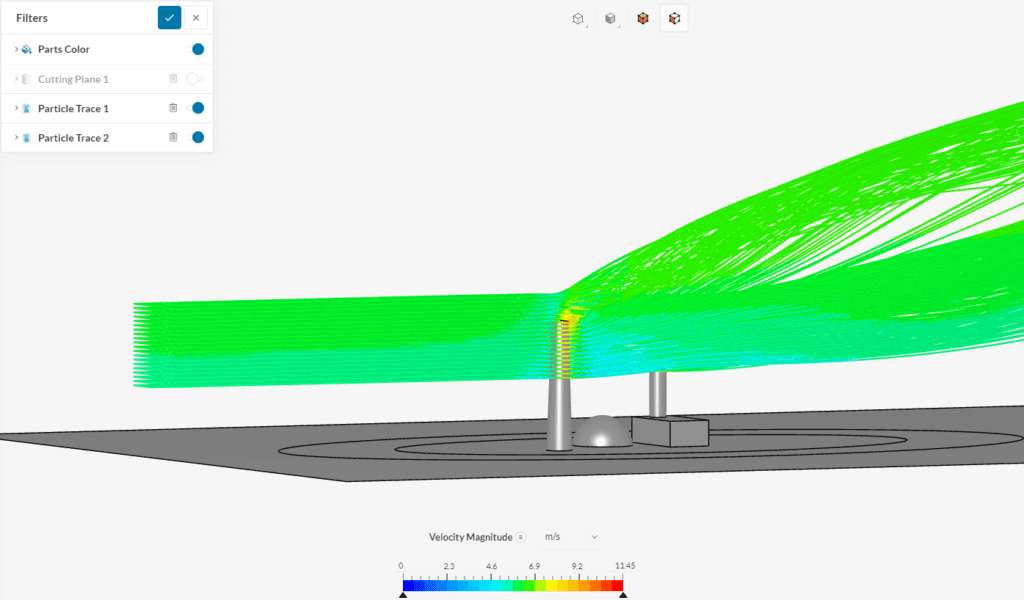
smoke propagation particle results — Figure 35: Particle traces aligned with the chimneys with the flow rising due to gas coming out of the chimney. The hot air rises to the top with a suction effect to the lower airflow.

Based on Figure 36, the gas coming out of the chimneys causes the flow to rise and creates a higher velocity.

5.3 Cutting Plane

Next, let’s utilize a cutting plane generated by default to observe how the smoke propagation, or gas coming out of the chimneys, affects the temperature of the surroundings. Toggle the ‘Cutting Plane’ on and the ‘Particle Traces’ off. Set up the settings of the cutting plane by following the step below:

Under Position, change the cutting plane placement by typing in the following coordinates: ’50, 0.85, 25′.
The Orientation of the cutting plane should be in the ‘Y’ axis.
Furthermore, please enable the velocity vectors with the on/off toggle next to Vectors.
To improve the visualization, change the vectors’ Coloring to a black ‘Solid color’.
Reduce the Scale factor to ‘0.01’ and the Spacing to ‘0.005’.
To increase the visibility turn on the ‘Project vectors onto plane’.

smoke propagation cutting plane settings — Figure 36: Cutting plane in the **‘Y-axis’** with velocity vectors

After adjusting the setting the result should look similar to this:

smoke propagation cutting plane results — Figure 37: Cutting plane results. The flow of the air stream can be displayed via vectors.

From the figure above, we can see that hot gas comes out of the chimney, affecting the air temperature downstream. The buoyancy effects are also noticeable, with the hot exhaust air quickly rising towards the top of the enclosure.

5.4 Iso Volume

The final filter that will be showcased is the Iso volume filter which is very useful to observe the propagation of the gases. Please follow the steps below to set an iso volume filter:

Click the ‘Iso Volume’ button in the Filters panel.
Change the Iso scalar and Coloring to ‘Passive scalar 1’ and the Min. iso value range to ‘0.1’ and the Max iso value to ‘1’. With these settings, we are going to highlight the volumes which consist of 10% to 100% of exhaust gases.

The settings for the Iso Volume 1 can be seen in the figure below:

smoke propagation iso volume setting — Figure 38: Isovolume settings for the Passive Scalar 1

Follow the steps above for the gas coming out of the other chimney and changing the Iso scalar and Coloring to ‘Passive scalar 2’. The result should look similar to this:

smoke propagation iso volume results — Figure 39: Isovolumes of passive scalar coming from both chimneys in the range of **‘0.1’** to **‘1’**.

From Figure 39, you can see the smoke propagation results as the concentration of passive scalars. The Iso-Volume body displays the volume in which the smoke propagation is in a range from 0.1 to 1. It is evident that the smoke propagation is less than 10% as most of the higher concentration smoke remains at the boundary of the chimney outlet.

Analyze your smoke propagation results with the SimScale post-processor. Have a look at our post-processing guide to learn how to use the post-processor.

Congratulations! You finished the smoke propagation tutorial!

Have a look at the finished project

References

Yang, Yi, et al. “Consistent Inflow Boundary Conditions for Modelling the Neutral Equilibrium Atmospheric Boundary Layer for the SST k-ω Model.” Wind and Structures, vol. 24, no. 5, 2017, pp. 465–480., DOI:10.12989/was.2017.24.5.465.

Note

If you have questions or suggestions, please reach out either via the forum or contact us directly.

Last updated: October 10th, 2023

Did this article solve your issue?

How can we do better?

We appreciate and value your feedback.

Value	Formula
\((U)\) Velocity	(0.415/log((10+0.03)/0.03))/0.41log((z+0.03)/0.03)
\((k)\) Turb. kinetic energy	((0.41*5)/(log((10+0.03)/(0.03)))^2/(0.09)^0.5)
\( (\omega)\) Specific dissipation rate	(0.415/log((10+0.03)/0.03))/(0.41(0.09)^0.5)*1/(z+0.03)

Advanced Tutorial: Smoke Propagation From a Chimney

Overview

1. Prepare the CAD Model and Select the Analysis Type

1.2 Create the Simulation

2. Set up the Simulation

2.1 Define a Material

2.2 Model

2.2 Assign the Boundary Conditions

Formula for copy paste

2.3 Initial Conditions

2.4 Numerics and Simulation Control

2.5 Result Control

3. Mesh

3.1 Local Element Size Refinement

3.2 Inflate Boundary Layer Refinement

3.3 Region Refinement

4. Start the Smoke Propagation Simulation

5. Post-Processing

5.1 Result Controls

5.2 Particle Trace

5.3 Cutting Plane

5.4 Iso Volume

Did this article solve your issue?

How can we do better?

Contents

Platform

Resources

Community

About