Documentation
This article provides a step-by-step tutorial for the nonlinear structural simulation of the bending process for an aluminum pipe. The objective of this simulation is to analyze the deformation and stress distribution developed on the pipe during the process, including nonlinear phenomena such as material plasticity, physical contact, and large deformation.
This tutorial teaches how to:
We are following the typical SimScale workflow:
First of all, click the button below. It will copy the tutorial project containing the geometry of the aluminum pipe into your own workbench.
The following picture shows what should be visible after importing the tutorial project.
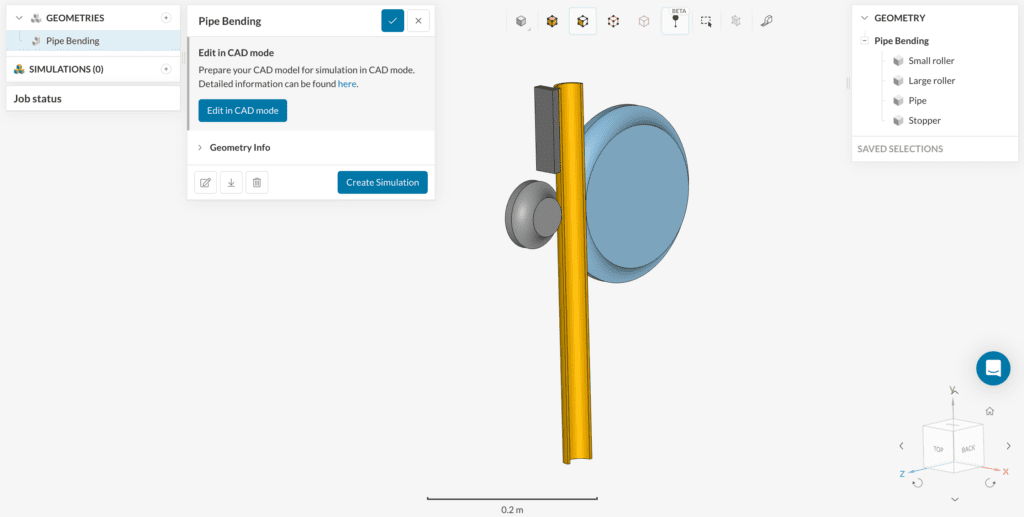
If you are using your own CAD model make sure to follow these instructions:
All solid geometry should be free of any interference, intersecting surfaces, and small edges. Issues such as these should be fixed in CAD before bringing the geometry into the SimScale platform. More specific preparation details are mentioned here.
Before starting to set up the model, check the following:
Hitting the ‘Create Simulation’ button leads to the following options:
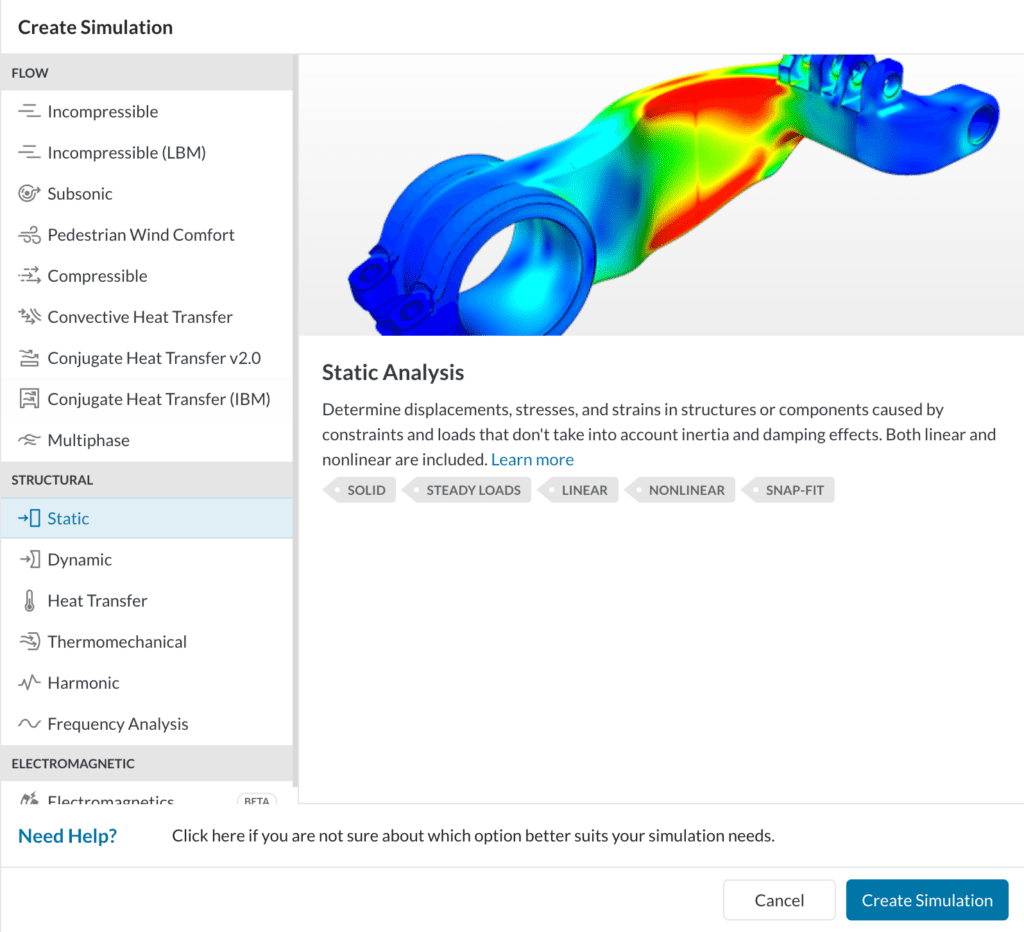
Choose ‘Static’ as analysis type and click on the new ‘Create Simulation‘ option to get started.
On the new simulation properties window that is opened, toggle on the ‘Non Linear analysis‘ option:
A static nonlinear analysis makes it possible to take into account phenomena such as:
This is done by ignoring inertia effects at the same time. This is different from a dynamic analysis, which would take into account inertial forces.
In this tutorial, we will simulate the forming process of an aluminum pipe via a hydraulic bending machine and analyze the mechanical stress and strain induced in the part(s). The following picture illustrates the parts of the model and the process:
The following modelling techniques will be used to simulate the process:
We will assign two contacts:
Beware that this is a difference because normal contacts are such that are representing ideal situations that would never appear like this in reality but can help simplify the simulation a lot. Physical contacts represent reality more accurately.
Check out this documentation page if you want to find out more about contacts.
SimScale automatically detects any touching faces within the geometry and assign bonded contacts. In this case all contacts are only on a line of touch, so the automatic detection fails with the following message:
In this case we can ignore the warning and just click on ‘ok’.
As our model needs a bonded contact between the pipe and the stopper, we are going to manually add it:
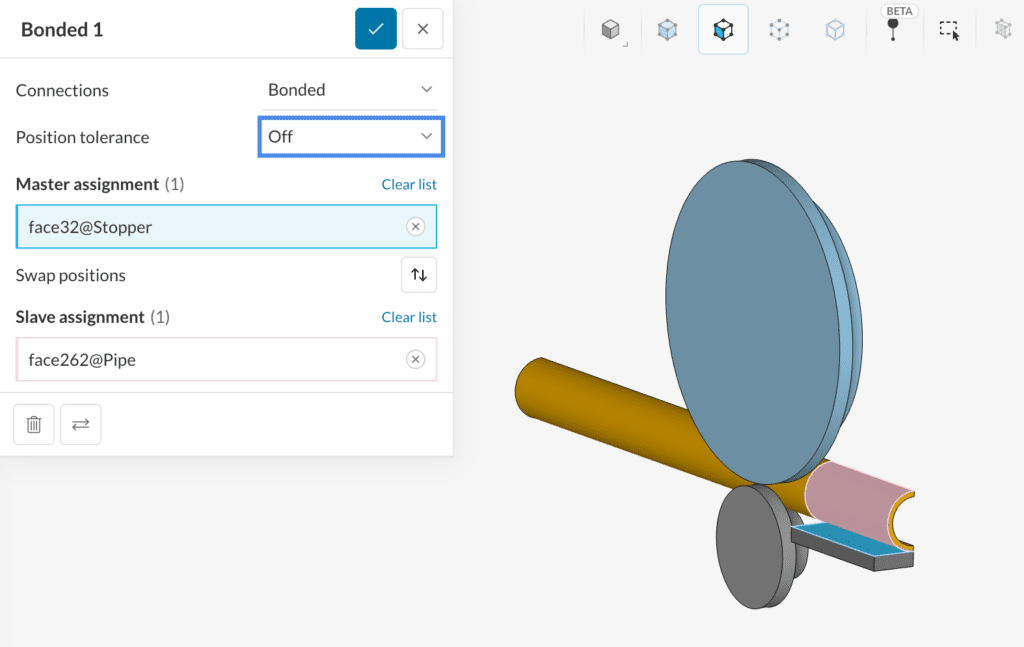
We now proceed to the Physical Contacts assignment. Physical contacts are used in touching surfaces that can slip, come into touch, separate, and transfer forces during the simulated process, such as the pipe and the rollers in our model. Friction effects can also be included, but they won’t be needed in this case. Follow the instructions below to create the physical contact model:
Note
If you are not sure about which surface to chose as a master and which as a slave for your own simulation, have a look at this knowledgebase article.
Leave those two panels as default, and proceed to the Materials item.
Two different materials are used for this simulation:
In order to create a new material, click the ‘+’ icon next to Materials. The materials library will be shown. Select the desired material from the list and click ‘Apply’ to create the material item, as shown in the picture:
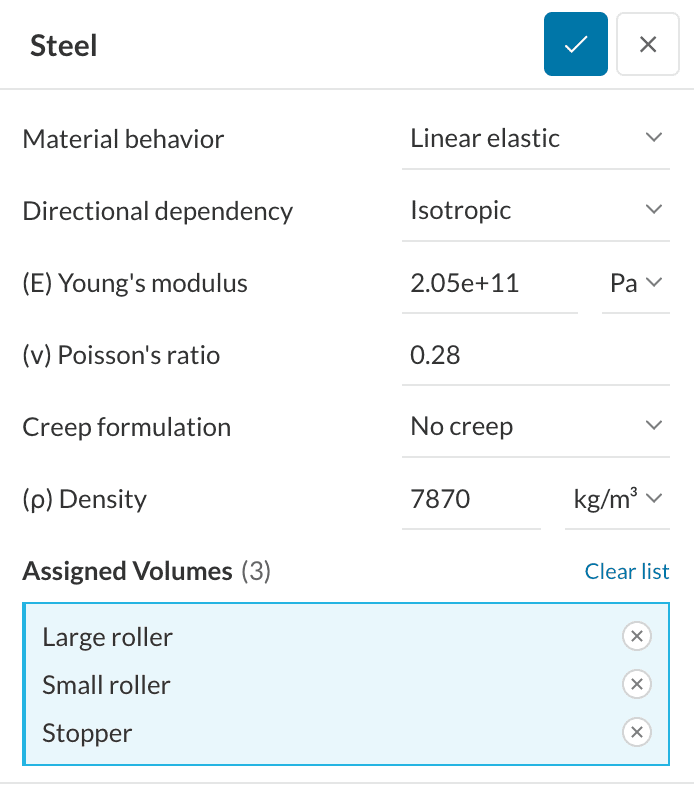
First create a Steel material item, which will be assigned to the Stopper, the Small roller, and the Large roller bodies. All other parameters can be left as default:
For the pipe, first create an Aluminium material, with the same procedure used for steel. Notice that the pipe body is automatically selected, as it is the only one left without material assignment.
The following picture illustrates the stress-strain curve of the material, which is known as an elastoplastic behavior. Changing the material behavior to plastic allows permanent deformation of the part, whereas the elastic behavior will cause the body to spring back to its original shape.

In order to model such non-linear behavior, change the Material behavior to ‘Elasto-plastic’, and set up the other parameters as shown. Notice that the stress curve
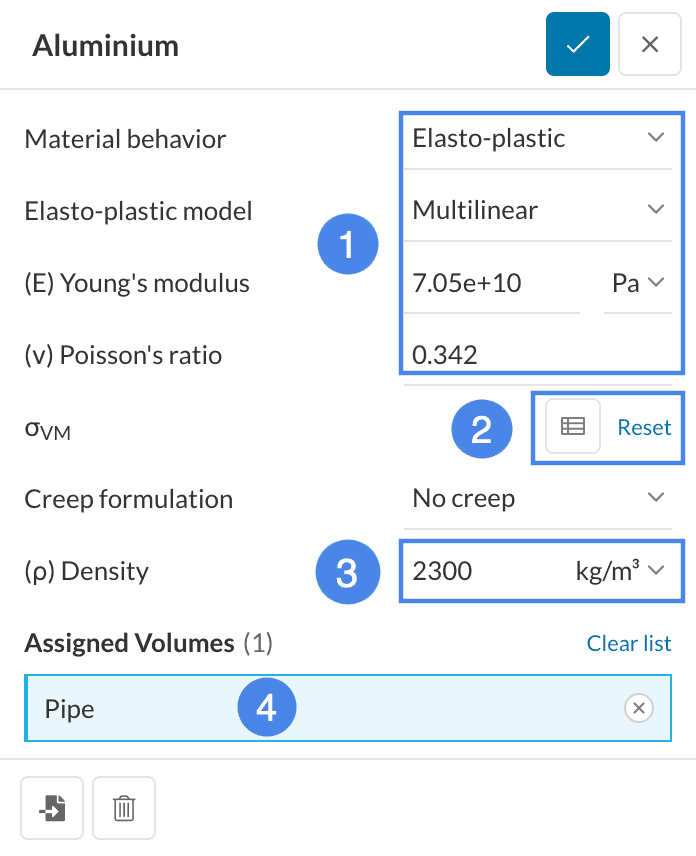
The solver needs the stress-strain curve, for aluminum pictured in Figure 12, for the material in order to predict the deformation. We will provide this curve in the form of a table. Use the following button to open the spreadsheet containing the curve data:
When you are on the spreadsheet, download the data to your computer in CSV format by going to File > Download > Comma-separated values.
Plastic Curve Data
If you examine or plot the CSV table, you will notice that it only includes the plastic part of the curve. That is, the [0,0] point is not in the curve, but it starts from the yielding point. This convention should always be followed when uploading data for a plastic curve.
Now click the table input button in the material window (highlighted in red in Figure 13). This will reveal the Specify value window:
Click the ‘Browse files’ button to select and upload the previously downloaded CSV file. The
Once you have uploaded this table, click the ‘Apply’ button in the settings from Figure 14 to accept the data and the ‘check-mark’ button on the material window (Figure 13) to save the setup. Note that the error message from Figure 13 should be gone by now.
For this simulation, the initial conditions can be left untouched.
Take a look at Figure 7 to get an overview of the physical situation and better understand what we are doing in this section.
In order to create a boundary condition, follow this procedure: click on the ‘+’ button option next to the ‘Boundary conditions‘ element at the left panel, and select the required boundary condition type from the drop-down menu, as shown in the figure:
Create a Fixed value boundary condition.
By default, we are in Face selection mode. In order to assign a Solid-body, you can use the scene tree at the right hand side of the workbench to activate the volume selection mode:
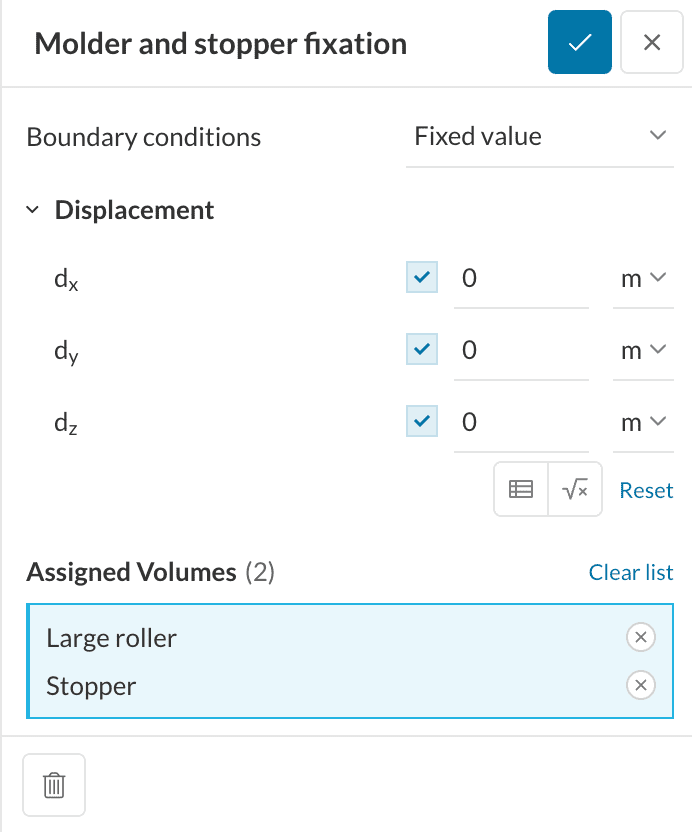
We need to assign it to the Large roller and Stopper bodies. Both of them have to be prevented from any movement, as presented in Figure 6.
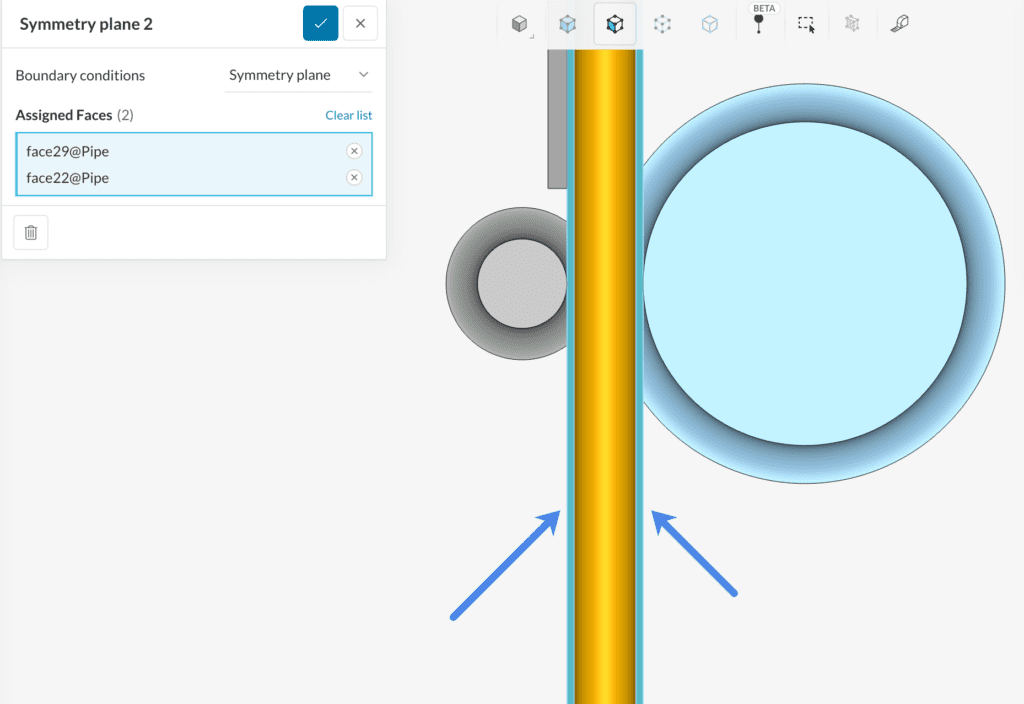
As you might have noticed, the geometry model includes only one-half of the pipe and the other bodies. This allows us to save on the mesh size and computation cost. A Symmetry plane boundary condition will be applied to the flat faces of the pipe (the other bodies have their degrees of freedom specified in the other boundary conditions, so no need to include them here). Create the boundary condition as explained above and assign the pipe symmetry faces as shown in the picture:
For the particular movement of the small roller, we will employ a Rotating motion boundary condition.
In our model, it happens that the axis of rotation passes through the origin, and is oriented in the X-direction. For a different model, the position and orientation of the rotation axis must be obtained from the CAD program and input in the boundary condition. Create the Rotating motion and assign the top face of the Small roller. Set up the parameters as shown:
In order to specify the rotation angle of the body, we will use a table input. It will go from zero to the maximum value in the simulated time, and the solver applies linear interpolation to the values in between. Take a look at the following image to remember what we are simulating:
It is important to take into account the right-hand rule and the direction of the rotation axis specified, to get the correct direction for the rotation. In this case, we want a positive 130° rotation of the roller to achieve the desired bending angle on the pipe.
| Time [s] | Rotation angle [°] |
|---|---|
| 0 | 0 |
| 1 | 130 |
In order to input the values, click the curve button from the rotating motion boundary condition window (highlighted in orange in Figure 20).
The Specify value window appears, just as in the material case, but this time with Formula and Table input options. Select the Table tab and input the values as shown:
Click the ‘Apply’ button (in Figure 22) and the ‘check-mark’ button (in Figure 20) to save the setup.
The Numerics parameters control the solver behavior and precision. In this case, we will only change one parameter: Convergence criteria. The default Relative criteria make use of the applied load magnitude to check the convergence of the computation. That is not possible in this simulation, because the model is driven by an imposed displacement so there are no loads. Accordingly, we need to change the criteria to Absolute, as shown in the picture:
The Simulation control parameters, on the other hand, specify the simulation time, time step, time adaptation and output write interval. Fill in the simulation control settings as below:
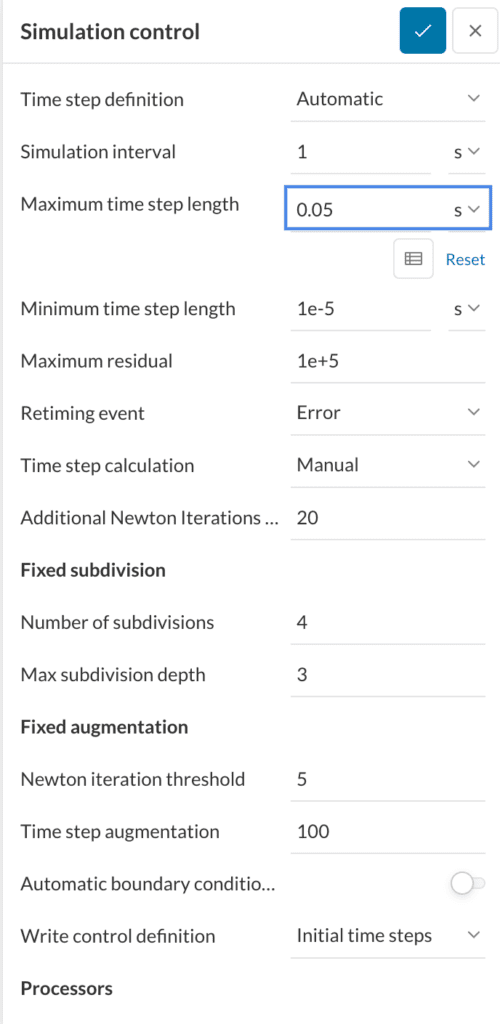
Result control allows us to query specific result fields from the simulation, such as displacements, strains and stresses, and their characteristics such as average or maximum values. A few default fields are provided, but in this case we will need to add more:
Two result fields will be queried from the solver that are not among the default ones:
In order to create the additional solution fields:
First, create a Stress field, and change the stress type to Signed von Mises stress.
Then, create a Contact field, and leave the default parameters:
Volume calculations are used to compute statistics of a field over a part, and are reported as curves over the simulation interval. In this case, two-volume calculations will be added:
In order to add a volume calculation, follow this steps:
Use the steps above to create a Volume calculation – Min-max item, and setup for the von Mises stress field over the pipe, as shown in the picture:
Repeat the steps to create the Signed von Mises Stress min-max item:
The standard mesh algorithm will be used. General settings can be left at their default values in this case:
Mesh refinements allow us to control the local size of elements over given faces and volumes. They are used primarily to optimize on computational resources: Instead of increasing the fineness globally, we assigning small element sizes only to regions of interest, which keeps the overall cell count smaller than if we would refine all the cells in the domain.
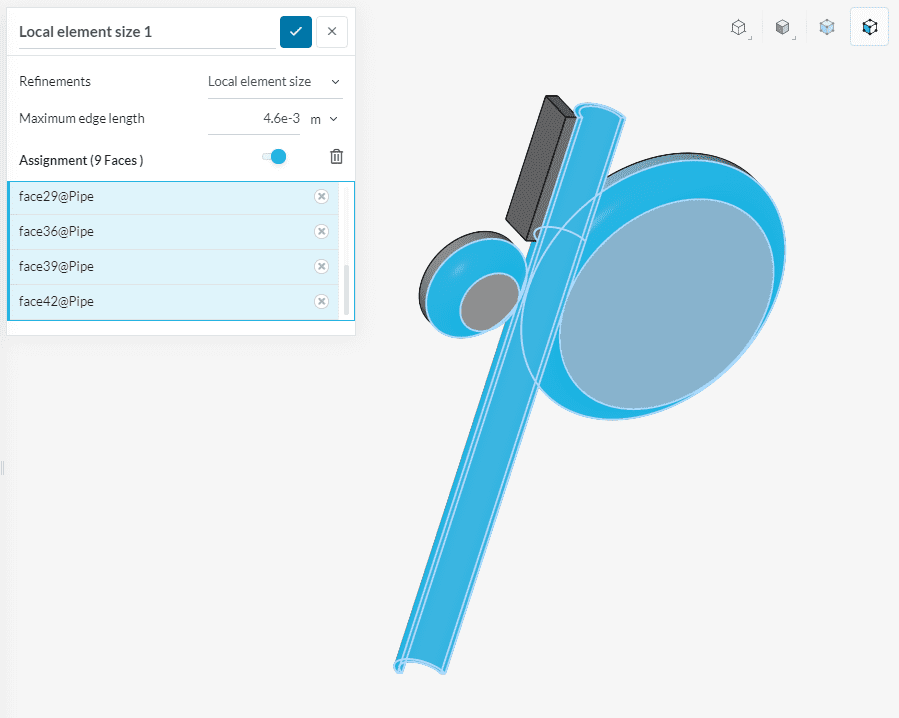
We will add one Local element size refinement:
The Local element size will be applied on the following faces:
Select the indicated faces (9 in total) from the viewer as shown in the picture, and then, apply a Maximum edge length of 4.6e-3
There is no need to generate the mesh at this point, because it will be computed as part of the simulation run. When the mesh computation is done, it will be marked with a green check-mark icon next to it. You can come back to it and view the resulting mesh:
Create a new computation run by clicking on the ‘+‘ icon next to the Simulation Runs on the tree, as shown below:
In the pop-up dialog, you can name and start the simulation run. After about one hour, you can have a look at the results.
Important
Once the simulation run is finished, you can post-process the pipe bending analysis results. To access the online post-processor you can use one of two methods:
Initially select the ‘Von Mises Stress’ as Coloring, and right-click on the colour bar to pick the ‘Use Continuous Scale‘ option. This will provide a smoother visualization of the results.
To visualize the deformation of the pipe and the movement of the parts, add a ‘Displacement‘ filter:
The following plot is displayed:
It can be noticed that the pipe followed the shape of the rig, and the bending was successfully captured.
You can see that the field selected by default is Von Mises Stress, which coincides with our goal. In order to make the legend scale easier to interpret, perform two changes:
Here we can see all the regions of the pipe that went past the yield point, coloured in red. The Hertzian contact stress on the follower body can also be appreciated.
The animation of bending process can also be visualized. To create the animation, add an Animation filter, the same way the Displacement filter was created:
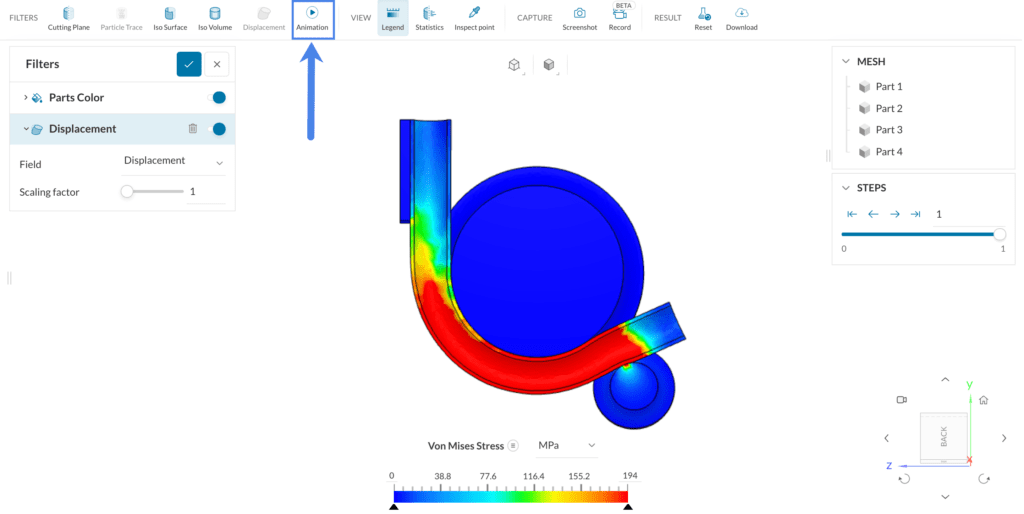
The default parameters for the filter are enough for our purpose:
Click the ‘Play’ button under Animation controls to start the animation of the bending process:
In order to better visualize the stress on the bent pipe, we want to hide all other parts. To do so, we follow this procedure:
The details of the stress distribution on the bent pipe can be seen without the obstruction of the other parts. In the plot, the higher stress levels occur in the outer portion of the pipe, close to the point of contact with the roller part.
Go ahead and try out for yourself what each one of the parameters does and what visualizations you can come up with. If you want to learn more about SimScale’s online post-processor, you can have a look at our post-processing guide.
Congratulations! You finished the tutorial!
Note
If you have any questions or suggestions, please reach out to us either via the forum or contact us directly.
Last updated: December 1st, 2023
We appreciate and value your feedback.
Sign up for SimScale
and start simulating now