websights

Fill out the form to download

Required field
Required field
Not a valid email address
Required field
Required field

  • Set up your own cloud-native simulation in minutes.

    • Documentation

    SimScale DocumentationSimulation SetupBoundary ConditionsCyclic Symmetry

    Cyclic Symmetry

    The cyclic symmetry boundary condition enables the modeling of a section of a 360° cyclic periodic structure and reduces the computation time and memory consumption considerably. Required settings include the center and axis of the cyclic symmetry as well as the sector angle. The master and slave surfaces define the cyclic periodicity boundaries.

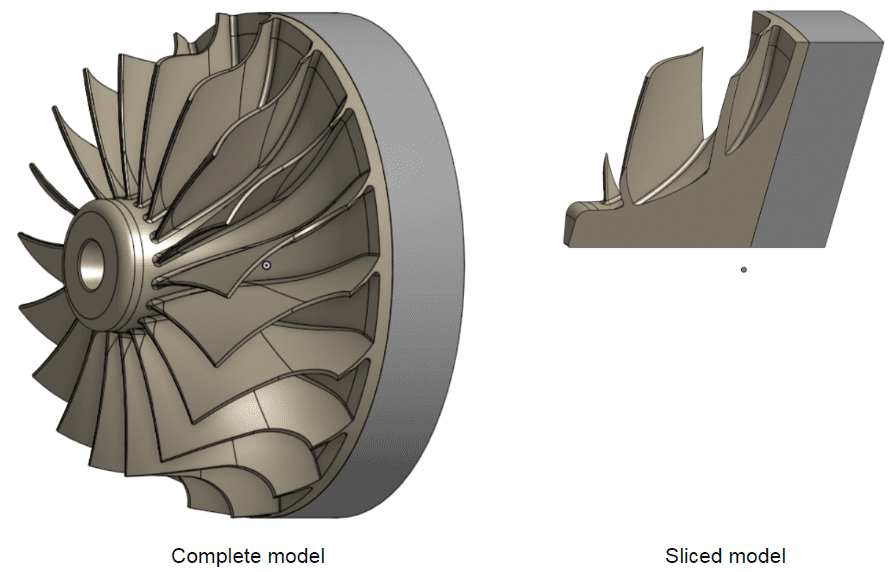
    comparison of the full and sliced model for a cyclic contract definition
    Figure 1: Comparison between a complete geometry and a sliced symmetry section of it

    Supported Analysis Types

    The following analysis types support the usage of this boundary condition:

    Defining in the Workbench

    The axis is defined by the Axis origin and the Axis direction. The definition of the Axis direction and the Sector angle has to be in accordance with the right-hand rule, such that it defines a rotation that starts on the slave surface and goes to the master surface. For a graphical example, see the picture below:

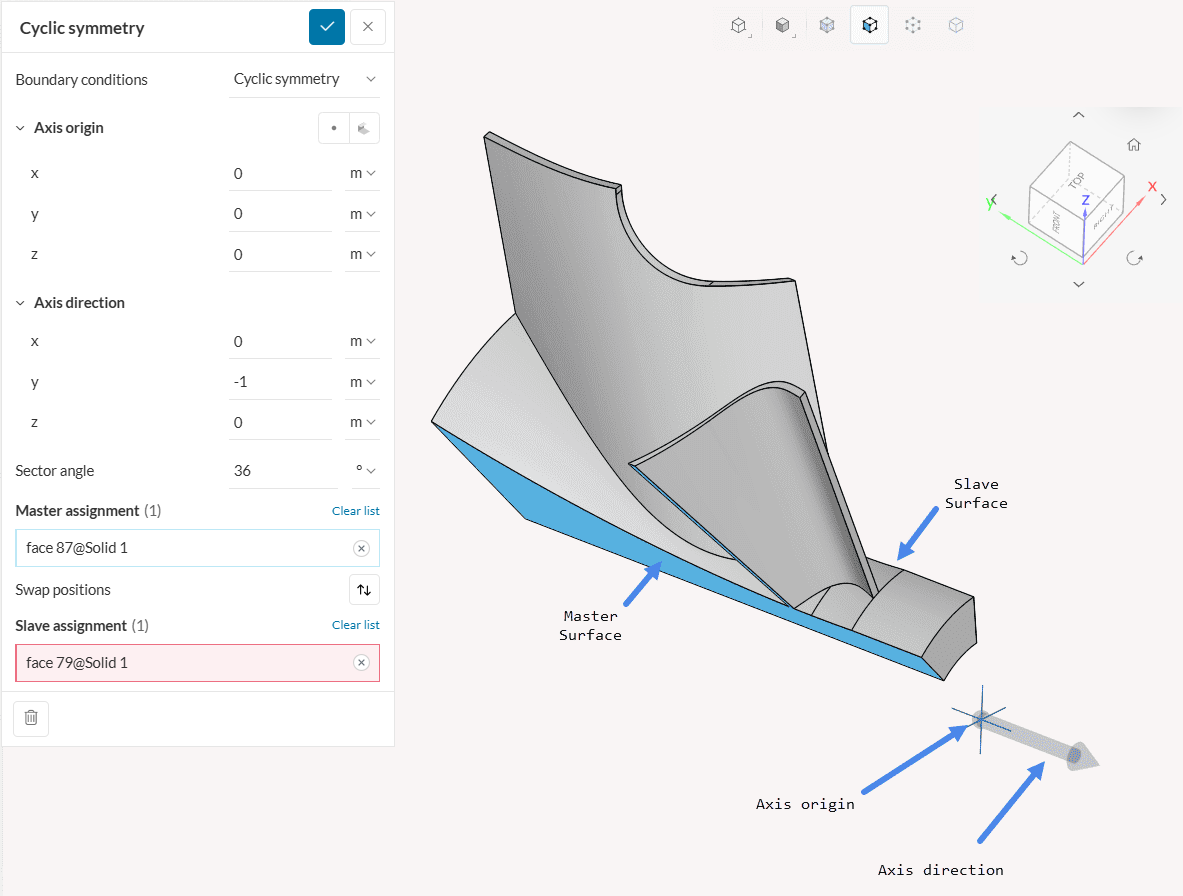
    cyclic symmetry linear contact panel example
    Figure 2: Illustration for a cyclic symmetry condition on a sliced geometry, showing the revolution axis origin, direction, and proper slave and master surfaces according to the right-hand rule.

    It’s required to define the axis of revolution and the sector angle explicitly. The Sector angle has to be given in degrees. Available ranges for the angle are from 0° to 180° and only values that divide 360° to an integer number are valid.

    Meshing for master and slave faces

    Generally, the more refined of the two periodic boundary surfaces should be chosen to be the Slave. In the case of cyclic symmetry, this will, in most cases, not matter since both faces should be meshed with nearly the same element sizes.

    The effect of the cyclic symmetry condition is to map the deformations of the master face onto the slave face, transforming them through the sector rotation. This creates the cyclic effect but does not constrain the body in the radial, tangential, or axial directions. Proper additional constraints must be added to prevent rigid body motions.

    cyclic symmetry contact example result in paraview
    Figure 3: Resulting Von Mises Stress on section (left) and transformed on the full 360° model (right) as viewed in Paraview.

    Important Information

  • All DOFs of the slave nodes will be constrained. Adding an additional constraint on those nodes could lead to an over-constrained system.
  • This is a linear constraint, so no large rotations or large deformations are allowed in the proximity of the cyclic symmetry boundaries.
  • A cyclic symmetry condition is only valid if geometry and loading conditions are symmetric around the axis of rotation.
  • The results reflect only the simulated portion. When a reaction force is calculated and displayed, the user needs to multiply the value of this sector model with the number of sectors for the full model to extract the corresponding value.
  • You should not use one cyclic contact for multiple solids, each should have their own, otherwise you might get unexpected connections of the edge of one body connecting with the other part, instead of its own counterpart.

    • Last updated: August 16th, 2024

    Contents