Documentation
Von Mises stress is a value used to determine if a given material will yield or fracture. It is mostly used for ductile materials, such as metals. The von Mises yield criterion states that if the von Mises stress of a material under load is equal to or greater than the yield limit of the same material under simple tension then the material will yield.
It is commonly accepted that the history of elasticity theory began with the studies of Robert Hooke in the 17th century\(^1\) who explored the fundamental concepts of the deformation of a spring and the displacement of a beam. However, engineering wasn’t the only reason for the study of elasticity theory, as that research was also linked to an attempt of interpreting the nature and the theory of ether\(^2\).
It was only in the 19th century that the quantitative and mathematical theory of the elasticity of bodies was born, together with continuum mechanics. This allowed the use of integral and differential calculus when modeling elastic phenomena. The continuum mechanics assumes homogenization of the medium, such, that microscopic fluctuations are averaged and a continuous field that models the medium can be obtained. Therefore, this implies that for every instant of time and every point in space occupied by the medium, there exists a punctual particle.
Many theories and concepts stem from the basic concept of continuum mechanics. One of those is the maximum distortion energy theory, which is applied in many fields, such as rubber bearings and applications with other ductile materials. It was Hubert who initially proposed it in 1904, and then von Mises developed it further in 1913\(^3\).
According to the maximum distortion energy theory, yielding occurs when the distortion energy reaches a critical value. This critical value, which is material specific, can be easily obtained through a simple tension test.
When a body, in an initial state of equilibrium or undeformed state, is subjected to a body force or a surface force, the body deforms correspondingly until it reaches a new state of mechanical equilibrium or deformed state. The inner body forces are the result of a force field such as gravity, while the surface forces are forces applied on the body through contact with other bodies.
The relations among external forces — which characterize what is called stress — and the deformation of the body, which characterizes strain, are called Stress-Strain relations. These relations represent properties of the material that compose the body and are also known as constitutive equations.
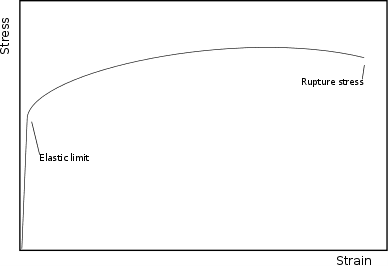
The figures below (adapted from [4]) illustrate the curve obtained when studying the strain response of the uniaxial tension of a mild steel beam. These will help us understand why von Mises is important. The description of each emphasized point is as follows:
This diagram is commonly approximated for many materials, as is shown in the picture below:
The elastic limits discussed before are based on simple tension or uniaxial stress experiments. The maximum distortion energy theory, however, originated when it was observed that materials, especially ductile ones, behaved differently when a non-simple tension or non-uniaxial stress was applied. They were exhibiting resistance values that were much larger than the ones observed during simple tension experiments. This led to the development of a new theory involving the full stress tensor.
The von Mises stress is a criterion for yielding widely used for metals and other ductile materials. It states that a body will yield if the stress components acting on it are greater than this threshold.\(^4\):
$$ \frac{1}{6}[(\tau_{11}-\tau_{22})^2 + (\tau_{22}-\tau_{33})^2 + (\tau_{33}-\tau_{11})^2 + 6(\tau^2_{12}+\tau^2_{23}+\tau^2_{13})]=k^2 \tag{1}$$
The constant \(k\) is defined through experiment, and \(\tau\) is the stress tensor. Common experiments for defining \(k\) are made from uniaxial stress, where the above expression reduces to:
$$ \frac{\tau^2_y}{3}=k^2 \tag{2}$$
If \(\tau_y\) reaches the simple tension elastic limit, \(S_y\), then the above expression becomes:
$$ \frac{S_y^2}{3}=k^2 \tag{3}$$
Which can be substituted into the first expression:
$$ \frac{1}{6}[(\tau_{11}-\tau_{22})^2 + (\tau_{22}-\tau_{33})^2 + (\tau_{33}-\tau_{11})^2 + 6(\tau^2_{12}+\tau^2_{23}+\tau^2_{13})]=\frac{S_y^2}{3} \tag{4}$$
or, finally
$$ \sqrt{\frac{(\tau_{11}-\tau_{22})^2 + (\tau_{22}-\tau_{33})^2 + (\tau_{33}-\tau_{11})^2 + 6(\tau^2_{12}+\tau^2_{23}+\tau^2_{13})}{2}}=S_y \tag{5}$$
The von Mises stress, \(\tau_v\), is defined as:
$$ \tau_v^2=3k^2 \tag{6}$$
Therefore, the von Mises yield criterion is also commonly rewritten as:
$$ \tau_v\geq{S_y} \tag{7}$$
That is, if the von Mises stress is greater than the simple tension yield limit stress, then the material is expected to yield.
The von Mises stress is not true stress. It is a theoretical value that allows the comparison between the general tridimensional stress with the uniaxial stress yield limit.
The von Mises yield criterion is also known as the octahedral yield criterion\(^5\). This is due to the fact that the shearing stress acting on the octahedral planes (i.e. eight planes forming an octahedron, whose normals form equal angles with the coordinate system) can be written as:
$$ \frac{1}{3}\sqrt{(\tau_1-\tau_2)^2 + (\tau_2-\tau_3)^2 + (\tau_3-\tau_1)^2}=\tau_{oct} \tag{8}$$
Which, for the case of uniaxial or simple tension, simplifies to:
$$ \frac{\sqrt2}{3}\tau_y=\tau_{oct} \tag{9}$$
Again, if \(\tau_y\) reaches the simple tension elastic limit, \(S_y\), then the above expression becomes:
$$ \frac{\sqrt2}{3}S_y=\tau_{oct} \tag{10}$$
And, by applying this result in the octahedral stress expression:
$$ \sqrt{\frac{(\tau_1-\tau_2)^2 + (\tau_2-\tau_3)^2 + (\tau_3-\tau_1)^2}{2}}=S_y \tag{11}$$
Similar to the result obtained for the von Mises stress, this defines a criterion based on the octahedral stress. Consequently, if the octahedral stress is greater than the simple stress yield limit, then yield is expected to occur.
The von Mises stress can, for example, be applied in fields such as drilling of hydrocarbon reservoirs, where pipes are expected to be under high pressure and combined loading conditions. In this case, the von Mises stress formula can be written as\(^5\):
$$ \sqrt{\frac{(\tau_z-\tau_t)^2 + (\tau_t-\tau_r)^2 + (\tau_r-\tau_z)^2}{2}}=\tau_v \tag{12}$$
Where \(z\), \(r\), and \(t\) are the axial, radial and tangential stresses. The criterion is the same as before, that is, if the von Mises stress obtained from the above expression is equal or greater than the simple tension yield stress of the material, then yielding is expected to occur.
The Tresca yield criterion is another example of a common criterion used for determining the maximum stress of material before yielding. Calculating yielding with Tresca’s method always results in a lower result compared to the von Mises method. It is commonly known as a more conservative estimate of failure within the science community. Also, it is known as the maximum shearing stress yield criterion\(^4\).
The most general expression for the maximum shearing stress is:
$$ [(\tau_1-\tau_2)^2-(S_y)^2][(\tau_2-\tau_3)^2-(S_y)^2][(\tau_3-\tau_1)^2-(S_y)^2]=0 \tag{13}$$
Knowing the ordering of the magnitude of the stress components helps simplify this criterion. The expression above now reduces to:
$$ (\tau_1-\tau_3)^2-(S_y)^2=0 \tag{14}$$
The Tresca yield criterion is piecewise linear, while the von Mises yield criterion is non-linear. However, the Tresca yield surface can involve singularities. The differences in predictions between the two conditions are relatively small.
There are many fields that benefit from the von Mises yield criterion. Feel free to browse through the public project library of SimScale to get a more practical grasp of the von Mises theory. For example, the animation below shows a study of the von Mises stress on a mounting plate subjected to a certain load.
The picture below is taken from a step-by-step tutorial that shows a structural and plasticity analysis for the burst of a gas tank and is an interesting resource for beginners.

Become a SimScale member!
Try our structural mechanics tutorials and observe the von Mises stresses yourself. Join SimScale today and experience cloud-based simulation like no other.
References
Last updated: August 11th, 2023
We appreciate and value your feedback.
What's Next
What is Natural Frequency?Sign up for SimScale
and start simulating now