Documentation
In the context of CFD modeling, an Atmospheric Boundary Layer (ABL) is an important aspect for modeling the flow around buildings, or for near-field dispersion problems. This can be relevant for many applications such as in Architecture, Pedestrian Wind Comfort (PWC), and Urban Planning. For a general description of the ABL, please refer to this article in our documentation.
This article explains how the ABL profile is generated with respect to the Wind Engineering Standards supported in the Pedestrian Wind Comfort simulation type in SimScale.
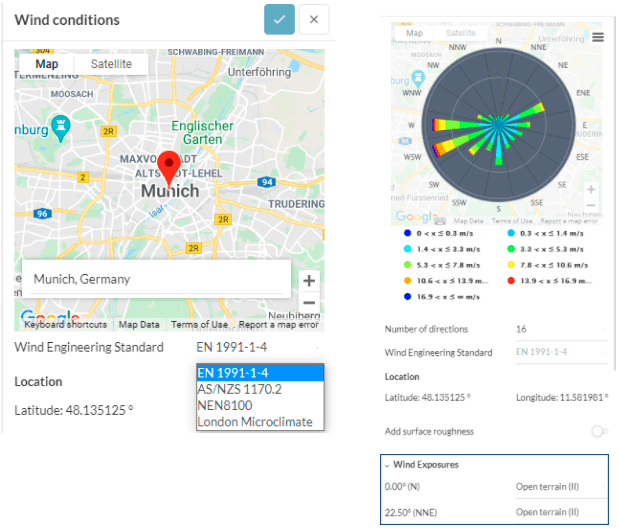
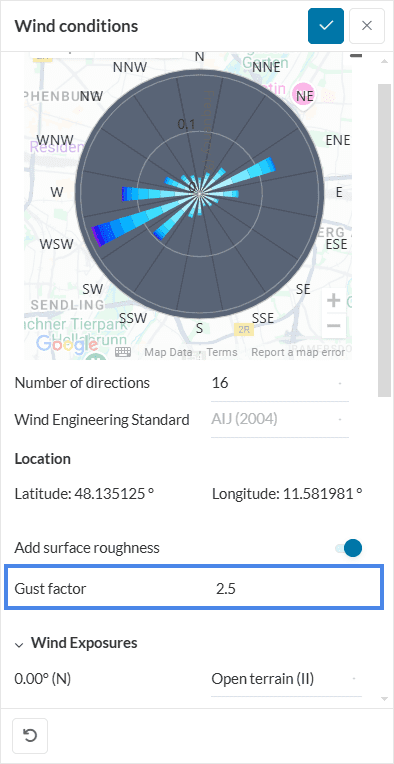
Before discussing the formulation utilized in generating the ABL, it is helpful to remember why and at which stage in a PWC simulation this is needed. When specifying the wind conditions you will be prompted with the choice of a wind engineering standard and a wind exposure category that will basically define how your ABL profile would look like coming from that particular direction of your terrain. See Figure 1 below for a snapshot of the interface illustrating this step.
The general formulations used to model the ground normal profiles such as velocity, turbulent kinetic energy (TKE) and the dissipation rate are based on [1,2,3].
$$ u = \frac{u^*}{\kappa} \ln{\left(\frac{z – d + z_0}{z_0}\right)} \tag{1} $$
$$ v = 0 ;w = 0 $$
Important
The AS/NZS 1170.2 and the City of London (CoL) guidelines use a different approach to model the wind velocity profile, which is based on the Harris and Deaves boundary layer models. See section 2.2 and 2.4 for a description on the model used.
$$ u^* = \frac{u_{ref}\kappa}{\ln\frac{z_{ref} + z_{0}}{ z_{0}}}\tag{2} $$
Where
| $$u$$ | Ground-normal streamwise flow speed profile [\(m/s\)] |
| $$v$$ | Spanwise flow speed [\(m/s\)] |
| $$w$$ | Ground-normal flow speed [\(m/s\)] |
| $$u^*$$ | Friction velocity [\(m/s\)] |
| $$\kappa$$ | von Kármán constant = 0.41 |
| $$z$$ | Ground-normal coordinate component [\(m\)] |
| $$d$$ | Ground-normal displacement height [\(m\)] |
| $$z_{0}$$ | Aerodynamic roughness length [\(m\)] |
| $$u_{ref}$$ | Reference mean streamwise wind speed at \(z_{ref}\) [\(m/s\)] |
| $$z_{ref}$$ | Reference height being used in u∗ estimations [\(m\)] |
Displacement Height \((d)\)
According to [4] the displacement height \(d\) is relevant for flows over forests and cities. “The displacement height gives the vertical displacement of the entire flow regime over areas which are densely covered with obstacles such as trees or buildings.”
$$ k = \frac{(u^*)^2}{\sqrt{C_{\mu}}} \sqrt{C_{1} \ln{\left(\frac{z – d + z_0}{z_0}\right)} + C_{2}}\tag{3}$$
$$ \epsilon = \frac{(u^*)^3}{\kappa ( z – d + z_0 )} \sqrt{C_{1} \ln{\left(\frac{z – d + z_0}{z_0}\right)} + C_{2}}\tag{4} $$
$$ \omega = \frac{u^*}{\kappa \sqrt{C_{\mu}}} \frac{1}{ z – d + z_0 }\tag{5} $$
Note
To produce a uniform TKE, the values for \(C_1\) and \(C_2\) are assumed to be by default 0 and 1, respectively. And the displacement height d is assumed to be 0.
$$k = \sqrt{D_1 \ln{\left(\frac{z + z_0}{z_0}\right)} + D_2 }\tag{6} $$
$$D_1= \left(\frac{(u^*)^2}{\sqrt{C_{\mu}}}\right)^2 C_1 \tag{7} $$
$$D_2= \left(\frac{(u^*)^2}{\sqrt{C_{\mu}}}\right)^2 C_2 \tag{8} $$
Where
| $$ k $$ | Ground-normal turbulent kinetic energy (TKE) profile \([m^2/s^2]\) |
| $$\epsilon$$ | Ground-normal TKE dissipation rate profile \([m^2/s^3]\) |
| $$\omega$$ | Ground-normal specific dissipation rate profile \([m^2/s^3]\) |
| $$C_{\mu}$$ | Empirical model constant = 0.09 |
| $$C_1$$ | Curve-fitting coefficient for profiles |
| $$C_2$$ | Curve-fitting coefficient for profiles |
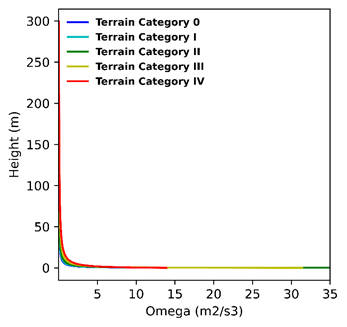
Figure 2 below, illustrates how the shape of the ABL profile changes with respect to the terrain category. The following section elaborates more on how these profiles differ for each wind engineering standard.
When choosing one of the Wind Engineering Standards for your PWC simulation, the values of the variables in the ABL equations above vary depending on the exposure category. As shown above in Figure 2, the variability of the mean wind velocity depends on:
Each Wind Engineering Standard defines different values that associate best with the exposure category of that particular region.
Reference velocity and height
For generating the ABL profiles that follows, a reference velocity and a reference height of 10 \( m/s\) and 10 \( m\) had been used, respectively. In case of a custom terrain, there is not a single global \(z=0\) to use as a reference for the velocity profile, but it rather depends on the topology of the terrain.
Table 3 shows the six general exposure categories that are mostly used among wind engineering standards. Each wind engineering standard supplies different values of the ground surface roughness \(z_0\) either for all or some of these categories.
| General Exposure Category | Description |
| EC1 | City center with heavy concentration of tall building |
| EC2 | General urban area |
| EC3 | Suburban area |
| EC4 | Open terrain area |
| EC5 | Open lake or land with minimal obstruction |
| EC6 | Sea or coastal area |
Let’s discuss the Wind Engineering Standards supported within SimScale
The value of the aerodynamic roughness length \(z_0\) depending on the terrain category is shown in the table below. Moreover, the Eurocode does not provide values for the general exposure category EC1.
| Category | Description | $$z_0$$ [\(m\)] | Category name in Simscale Workbench |
| EC2 | General urban area | 1 | IV (Urban area) |
| EC3 | Suburban area | 0.3 | III ( Suburban area) |
| EC4 | Open terrain area | 0.05 | II (Open terrain) |
| EC5 | Open lake or land with minimal obstruction | 0.01 | I (Flat terrain) |
| EC6 | Sea or coastal area | 0.003 | 0 (Coastal area) |
The ABL profiles for velocity, TKE, and specific dissipation rate which had been generated with a log law profile can be seen below for each terrain category:
The mean wind velocity profile is modeled using the Deaves and Harris approach. This model simulates a logarithmic atmospheric boundary layer profile as follows [6]:
$$ \bar{u} = \frac{u^*}{0.4} \left[\ln{\left(\frac{z}{z_0}\right)} + 5.75 \left(\frac{z}{z_g}\right) – 1.88 \left(\frac{z}{z_g}\right)^2 -1.33 \left(\frac{z}{z_g}\right)^3 +0.25 \left(\frac{z}{z_g}\right)^4 \right]\tag{9}$$
Where
| $$ \bar{u} $$ | Design hourly mean wind speed at height \(z\) \([m/s]\) |
| $$ z $$ | The distance or height above ground \(m\) |
| $$ z_0 $$ | Aerodynamic roughness length [\(m\)] |
| $$ z_g $$ | The gradient height = \(\frac{u^*}{B * f}\) |
| $$ f $$ | Coriolis Parameter = 0.0001 |
| $$B$$ | 6 |
\(u^*\), \(k\), and \(\omega\)
The formulations used to model these parameters are the same as in equations 2, 3, and 5, respectively.
Regarding the terrain categories in the AS/NZS standard there exists one difference to the Euro Code. The AS/NZS standard provides values for EC1 (heavy concentration of tall buildings) but not for EC2 (general urban area).
| Category | Description | $$z_0$$ [\(m\)] | Category name in Simscale Workbench |
| EC1 | City center with heavy concentration of tall buildings | 2 | City center |
| EC3 | Suburban area | 0.2 | Suburban area |
| EC4 | Open terrain area | 0.02 | Open terrain |
| EC5 | Open lake or land with minimal obstruction | 0.002 | Flat terrain |
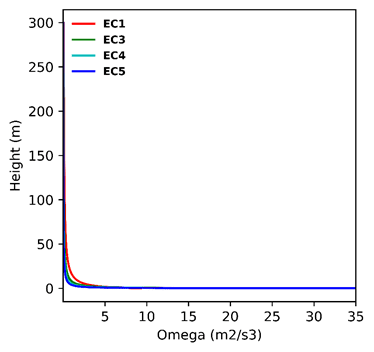
The following plots illustrate how the velocity, TKE, and specific dissipation rate looks like for each of the terrain categories of the AS/NZS defined above:
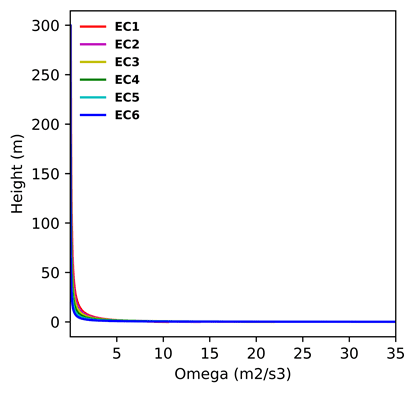
For the NEN8100 Dutch standard the following 6 terrain categories are available in SimScale and they are as follows:
| Category | Description | $$z_0$$ [\(m\)] | Category name in Simscale Workbench |
| EC1 | City center with heavy concentration of tall buildings | 2 | City center |
| EC2 | General urban area or forest | 1 | Urban or Forest |
| EC3 | Suburban area | 0.5 | Suburban |
| EC4 | Open terrain area (Rough) | 0.25 | Rough |
| EC5 | Open lake or land with minimal obstruction | 0.03 | Open |
| EC6 | Sea or coastal area | 0.0002 | Sea |
Due to the fact that the NEN8100 code utilizes a height of 60 \(m\) instead of 10 \(m\) as a reference height, a correction needs to be applied. More details can be found in the correction factors section in this documentation.
Below the ABL profile of velocity, TKE and specific dissipation can be seen:
The City of London wind standard models the variation of the mean and gust wind speed profiles based on the Harris and Deaves boundary layer models in the UK National Annex to the Eurocode.
$$ u (z) = \frac{u^*}{\kappa} \left[\ln{\left(\frac{z}{z_0}\right)} + 5.75 \left(\frac{z}{h}\right) – 1.88 \left(\frac{z}{h}\right)^2 -1.33 \left(\frac{z}{h}\right)^3 +0.25 \left(\frac{z}{h}\right)^4 \right]\tag{10}$$
Where
| \(h\) | Height of the neutral boundary layer = \( \frac{u^*}{B f}\) |
| \(f\) | Coriolis Parameter = 0.00011415 |
| \(B\) | 6 |
The model equation and the values for \(B\) and \(f\) provided above are based on [10,11,12].
\(u^*\) , \(k\), and \(\omega\)
The formulations used to model these parameters are the same as in equations 2, 3, and 5, respectively.
Furthermore, the roughness height values as a function of the exposure category for the London City wind standard are shown in the table below:
| Category | Description | $$z_0$$ [\(m\)] | Category name in Simscale Workbench |
| EC1 | City center with heavy concentration of tall buildings | 1 | Urban |
| EC2 | General urban area or forest | 0.5 | London City |
| EC3 | Suburban area | 0.3 | Suburban |
| EC4 | Open terrain area (Rough) | 0.05 | Open |
| EC5 | Open lake or land with minimal obstruction | 0.01 | Flat |
The ABL profiles depending on the values above are as follows:

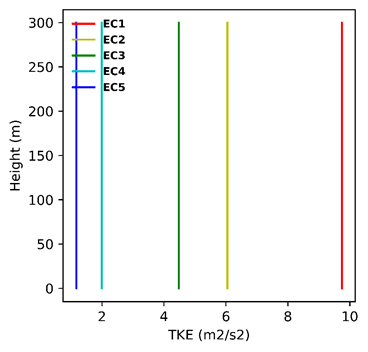
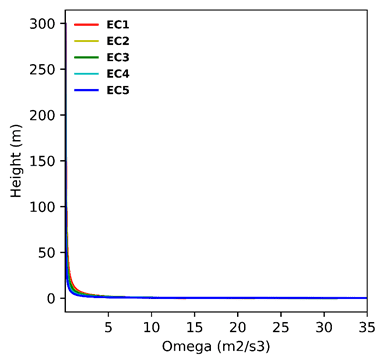
The main difference between the AIJ wind standard and the four standards discussed above is, that the AIJ ABL profile is based on Power law and not a Log law. A Gust factor also needs to be specified when defining wind conditions.
The roughness height values as a function of the exposure category for the AIJ (2004) wind standard are shown in the table below:
| Category | Description | alpha \(\alpha\) | \(z_0\) fitted at 10 \([m]\) | \(z_0\) fitted at 2 \([m]\) | Category name in Simscale Workbench |
| EC1 | An urban area densely populated with high-rise buildings (10 floors or more). | 0.35 | 4.44 | 2.335 | City Center (V, \(\alpha\) = 0.35 ) |
| EC2 | An urban area primarily composed of mid-rise buildings (4 to 9 floors). | 0.27 | 2.135 | 1.100 | Urban (IV, \(\alpha\) = 0.27) |
| EC3 | An area with numerous trees and low-rise buildings, or an area scattered with mid-rise buildings (4 to 9 floors). | 0.2 | 0.975 | 0.495 | Suburban (III, \(\alpha\) = 0.2) |
| EC4 | An area with obstacles similar to crops, like pastoral regions or grasslands, and areas scattered with trees and low-rise buildings. | 0.15 | 0.485 | 0.240 | Open (II, \(\alpha\) = 0.15) |
| EC5 | An area with few obstacles, such as a coastline or the surface of a lake. | 0.1 | 0.215 | 0.100 | Flat (I, \(\alpha\) = 0.1) |
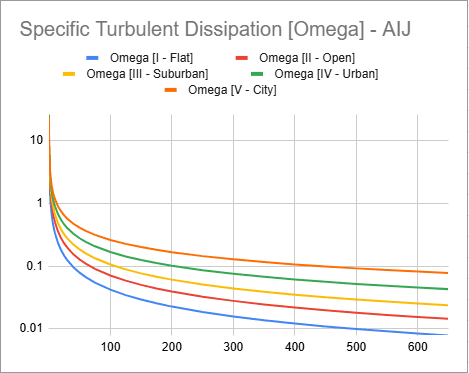
Inlet profiles for the AIJ (2004) can be found below:
Consistent with the other Wind Engineering Standards, SimScale runs the CFD analysis with a fixed reference speed of 10 \(m/s\) at the reference height of 10 \(m\).
To be consistent and to ensure numerical stability SimScale does not use the blending height \(z_b\) values provided by AIJ, but keeps them all at 0 \(m\) and has a full power law profile down to 0 \(m\).
$$U_z = 10 \left(\frac{z_{min}}{10}\right)^\alpha …….. z < z_{min} \tag{11.1}$$
$$U_z = 10 \left(\frac{z}{10}\right)^\alpha …….. z_{min} < z < z_G \tag{11.2}$$
$$U_z = 10 \left(\frac{z_G}{10}\right)^\alpha …….. z >= z_G \tag{11.3}$$
where \(\alpha\) and \(z_G\) are given in the table below.
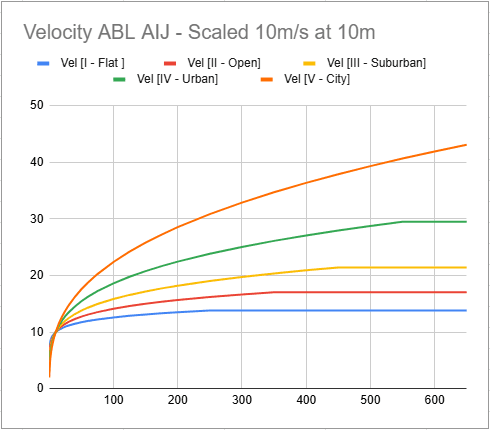
$$I_z = 0.1 \left(\frac{z_{min}}{z_G}\right)^{-\ \alpha -\ 0.05} ………z < z_{min} \tag{12.1}$$
$$I_z = 0.1 \left(\frac{z}{z_G}\right)^{-\ \alpha -\ 0.05} ………z_{min} < z < z_G \tag{12.2}$$
$$I_z = 0.1 ……. z >= z_G \tag{12.3}$$
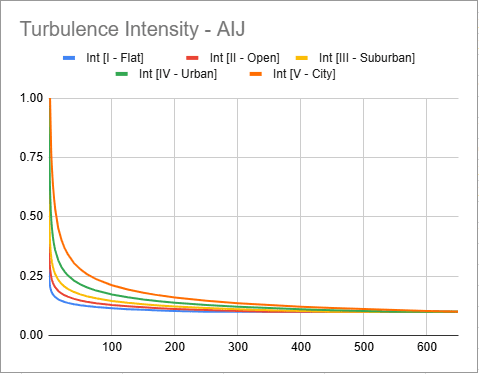
We can derive the Omega profile from the inlet form the TKE, velocity and viscosity data using the following formula (see AIJ doi:10.1016/j.jweia.2008.02.058):
$$\omega(z) = \frac{\epsilon(z)}{C_{\mu}\ k(z)} $$
$$\epsilon(z) = C_{\mu}^{1/2}\ k(z)\ \frac{U_{ref}}{z_{ref}} \alpha \left(\frac{z}{z_{ref}}\right)^{(\alpha -\ 1)} $$
Combining both formulas, we get:
$$\omega(z) = C_{\mu}^{-1/2}\ \frac{U_{ref}}{z_{ref}} \alpha \left(\frac{z}{z_{ref}}\right)^{(\alpha – 1)} \tag{13}$$
Adding in the reference height of 10 \(m\) and reference velocity of 10 \(m/s\) we get:
$$ \omega(z) = C_{\mu}^{-1/2} \alpha \left(\frac{z}{10}\right)^{(\alpha – 1)} \tag{14}$$
To assess a PWC study, three different types of information are needed:
The transformation of the statistical meteorological data to the location of interest at the building site is realized through the aerodynamic information, which is split into two parts:
Understanding this is the basis for the evaluation of pedestrian comfort, to do so, the local wind velocity needs to be related to the weather station data in order to obtain the probability of the local wind speed exceeding the threshold wind speeds defined by the comfort criterion.
The relation between the measured wind speed at the meteorological station \(u_{meteo}\) to the local wind speed \(u_{loc}\) is defined as the “wind amplification factor”:
$$ \gamma = \frac{u_{loc}}{u_{meteo}}\tag{15} $$
This can be split up in two components:
$$ \gamma = \frac{u_{loc}}{u_{meteo}} = \frac{u_{loc}}{u_0} * \frac{u_0}{u_{meteo}} \tag{16} $$
The figure below illustrates this further. (Note: \(u_{pot}\) refers to \(u_{meteo}\) in the figure)
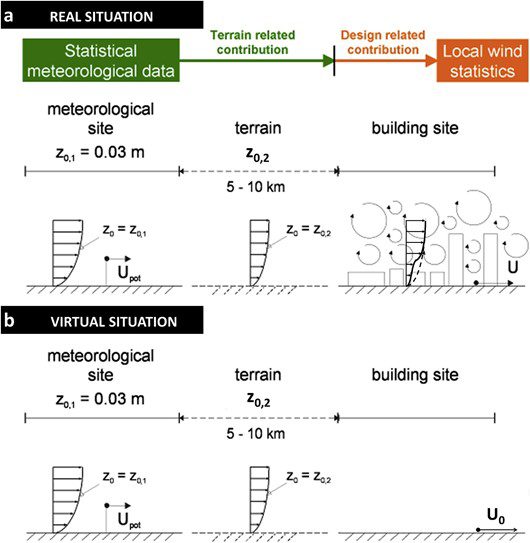
From the CFD analysis we get the first part \( \frac{u_{loc}}{u_0}\) directly. However, the correction of the weather station data \(\frac{u_0}{u_{meteo}}\) requires additional effort and calculations, which can differ between each wind engineering standard.
The wind comfort standards define limits that are related to the threshold local air speeds based on the type of activity. These limits cannot be exceeded for more than a specified percentage of time in a year.
For example, the table below illustrates the comfort levels based on the Lawson comfort criteria:
A meteorological wind station provides a discrete set of wind data, therefore in order to evaluate the probabilities of exceedance at any given threshold speed, the discrete set of data is fitted into a continuous one by the mean of a Weibull probability distribution.
Moreover, from the CFD simulation, we receive the locally measured wind speeds, and by using them with the combination of the parameters inside the Weibull probability distribution function, the probability of exceeding a certain wind speed at a specific location can be obtained. The City of London guidelines defines the Weibull function as:
$$ f(x) = P . e^{(-\frac xc)^k} \tag{17} $$
Where
| \(f\) | Frequency |
| \(P\) | The probability that the wind will approach from a certain direction |
| \(x\) | A given wind speed [m/s] |
| \(c\) | Scale factor |
| \(k\) | Shape factor |
Now we understand how the comfort criteria is evaluated. Nevertheless, a correction to the wind speed value inside the Weibull function is necessary to take into account the aerodynamic information discussed earlier in the preceding section. The correction values are incorporated in terms of the wind amplification factor inside equation 15, by multiplying with the scale factor \(c\) inside the Weibull probability distribution function. (refer to the example section below for an overview of the calculation method)
Since each wind engineering standard utilizes slightly different methods in conducting the design one has to account for these variations through correction factors. Corrections for the averaging time of the velocity or terrain exposure correction factor are some examples of possible corrections to be carried out.
For the EU standard the logarithmic boundary profile is valid until a maximum height of \(z_b\) = 200 \(m\), so we are also assuming this height as the blending height for all categories. This leads to the following :
Blending Height
Blending height refers to the height where the terrain effects are negligible and irrespective of the terrain the same speed is present. Which yields:
\(u_{meteo} \ (z_b) = u_0 \ (z_b)\)
$$ \gamma = \frac{u_{loc}}{u_{meteo}} = \frac{u_{loc}}{u_0} * \frac{u_0}{u_{meteo}} $$
The term \( \frac{u_{loc}}{u_0}\) can be calculated directly from the CFD simulation, where \(u_{loc}\) represents the local measured velocity at the location of interest, and \(u_0\) is the velocity at defined reference height 10 \(m/s\) at 10 \(m \) height.
$$ \frac{u_0}{u_{meteo}} = \frac{u_0 (z_b= 200 m)} {u_{meteo} (z_b= 200 m)}\tag{18} $$
$$ \frac{u_0}{u_{meteo}} = \frac{{u_0}^* \ln{ |\frac{z_b}{{z_{0}}}+ 1 }|} {{u_{meteo}}^* \ln{ |\frac{z_b}{{z_{0}}_{meteo}}+ 1 }| } \tag{19}$$
Inserting the formula of \(u^*\) into the equation above and centering it at 1 for EC4 (the terrain category of the meteorological station) results in:
$$ \frac{u_0}{u_{meteo}} = \frac{ln{ |\frac{z_{ref}}{{z_{0}}}+ 1 }|} {ln{ |\frac{z_{ref}}{{z_{0}}_{meteo}}+ 1 }| } * \frac{ln{ |\frac{z_{b}}{{z_{0}}_{meteo}}+ 1 }|} {ln{ |\frac{z_b}{{z_{0}}}+ 1 }|} \tag{20}$$
$$ \frac{u_0}{u_{meteo}} = \frac{ln{ |\frac{10}{{z_{0}}}+ 1 }|} {ln{ |\frac{10}{{z_{0}}_{meteo}}+ 1 }| } * \frac{ln{ |\frac{200}{{z_{0}}_{meteo}}+ 1 }|} {ln{ |\frac{200}{{z_{0}}}+ 1 }|} \tag{21}$$
The evaluation of the expression above for the different terrain categories yields the following correction factors as shown in the table below:
| Category | EC6 | EC5 | EC4 | EC3 | EC2 |
| Description | Coastal Area | Flat Terrain | Open Terrain | Suburban Area | Urban Area |
| Roughness \((z_0 [m])\) | 0.003 | 0.01 | 0.05 | 0.3 | 1 |
| Correction factor \((\frac{u_0}{u_{meteo}})\) | 1.14 | 1.09 | 1 | 0.85 | 0.707 |
Here the correction is directly related to the difference between the terrain category at which the meteorological data had been calculated and the terrain category at or near the building site.
As mentioned earlier, in order to evaluate the PWC we need to calculate the wind amplification factor which was split into two parts (see equations 15 and 16 above):
Since the meteorological data was calculated on terrain EC4 (open area terrain), it should have a factor of 1.0 (meaning that no correction is needed if the terrain category of the site of interest is also EC4).
The meteorological data is measured at 10 \(m\) height, and based on that one can read the values of the velocity profile multipliers for each terrain category (see table 5 above for the description of each terrain category) from the 1989 AS/NZS standard as :
Finally, we get the factor for each terrain category by centering the sequence above at 1.0 for EC4:
| Category | EC5 | EC4 | EC3 | EC1 |
| Description | Flat Terrain | Open Terrain | Suburban Area | City Center |
| Roughness \((z_0 [m])\) | 0.002 | 0.02 | 0.2 | 2 |
| Correction factor \((\frac{u_0}{u_{meteo}})\) | 1.183 | 1.0 | 0.733 | 0.583 |
The meteorological data for the NEN8100 wind standard is already corrected to the local roughness directly by the NEN8100 code. Therefore, no direct exposure correction needs to take place.
However, the wind speed data for NEN8100 is defined at 60 \(m\) height but in the context of the framework followed by SimScale a 10 \(m\) height for the reference velocity is utilized. Hence, a correction is needed to scale down to the 10 \(m\) reference height.
As we have,
$$ \frac{u_0}{u_{meteo}} = \frac{{u_0}^* \ln{ |\frac{10}{z_0}+ 1|}} {{u_{meteo}}^* \ln{ |\frac{60}{z_0}+ 1|}} = \frac{\ln{ |\frac{10}{z_0}+ 1|}} {\ln{ |\frac{60}{z_0}+ 1|}} \tag{22}$$
| Category | EC6 | EC5 | EC4 | EC3 | EC2 | EC1 |
| Description | Sea | Open | Rough | Suburban | Urban or Forest | City Center |
| Roughness \((z_0 [m])\) | 0.0002 | 0.03 | 0.25 | 0.5 | 1 | 2 |
| Correction factor$$(\frac{u_0}{u_{meteo}})$$ | 0.81910 | 0.76461 | 0.67707 | 0.63483 | 0.58331 | 0.52177 |
Note
These categories are not fully fixed by NEN8100, they are rather fitted to cover best the roughness appearing in the related NPR 6097 standard.
For the CoL standard, the weather data is given directly as Weibull coefficients and they relate to a reference height of 120 \(m\). No exposure correction is needed if the default CoL exposure (\(z_0\)=0.5 \(m\)) is used.
The relation between the measured wind speed at the inlet reference velocity \(u_{120m}\) to the local wind speed \(u_{loc}\) is defined as the “wind amplification factor” as stated before.
$$ \gamma = \frac{u_{loc}}{u_{120}} = \frac{u_{loc}}{u_0} * \frac{u_0}{u_{120}} $$
The first one being the local contribution of the topography close to the building, whereas the second part is the corrective factor for the wind data, which is usually given for a specific reference terrain category (here “London City” terrain with 0.5 \(m\) roughness).
From the CFD analysis we get the first part \(\frac{u_{loc}}{u_0}\) directly. On the other hand, the correction of the weather data \(\frac{u_0}{u_{120}}\) , requires some additional effort.
The atmospheric boundary layer profile is valid until a max height of \(z_g\) = \(h\) (gradient height from Deaves and Harris model), so we are assuming for consistency reasons that this height is also the blending height (using always the lower gradient height of the two categories in transition).
| Category | EC5 | EC4 | EC3 | EC2 | EC1 |
| Description | Flat | Open | Suburban | London City | Urban |
| Roughness \((z_0 [m])\) | 0.01 | 0.05 | 0.3 | 0.5 | 1 |
| Correction factor$$(\frac{u_0}{u_{120}})$$ | 1.17 | 1.14 | 1.05 | 1 | 0.87 |
The calculation for the Speedup factor gamma for the AIJ (2004) standard is given by:
$$ \gamma= \frac{u_{0}}{u_{meteo}} $$
Where a 10 \(m\) height for the reference velocity is utilized.
We assume the same velocity at the gradient height. For consistency, we use the lower of the two gradient heights as the intersection point.
| Category | EC5 | EC4 | EC3 | EC2 | EC1 |
| Description | Flat (I, \(\alpha\) = 0.1) | Open (II, \(\alpha\) = 0.15) | Suburban (III, \(\alpha\) = 0.2) | Urban (IV, \(\alpha\) = 0.27) | City Center (V, \(\alpha\) = 0.35) |
| Blending height \((z_b [m])\) | 5 | 5 | 5 | 10 | 10 |
| Gradient height \((z_G [m])\) | 250 | 350 | 450 | 550 | 650 |
| Correction factor wrt EC4 $$(\frac{u}{u_meteo})$$ | 1.175 | 1 | 0.837 | 0.653 | 0.491 |
This example demonstrates the calculation procedure for the comfort criteria. The necessary inputs for this are:
The steps for calculation are as follows:
Step 1:
$$ f(x) = P . e^{(-\frac uc)^k} $$
Step 2:
$$\frac{u_{loc}}{u_0}= \frac{8 \ m/s} {10 \ m/s} = 0.8 $$
Step 3:
$$ \frac{u_0}{u_{meteo}} = 0.58 $$
Step 4:
$$ \gamma= \frac{u_{loc}}{u_{meteo}} = 0.8 * 0.58=0.46 $$
Step 5:
$$ f(dir , u > 5 m/s ) = P_{dir} . e^{(-\frac{u}{c})^k} $$
$$ = P_{dir} . e^{-\left(\frac{5}{0.46c_{dir}}\right)^{k_{dir}}} $$
$$ = P_{dir} . e^{\left(-\frac{10.87}{c_{dir}}\right)^{k_{dir}}} $$
For the NEN8100 standard this would mean we are in category D (Walking Fast).
For Lawson we would need to check the exceedance probabilities for 1.8 \(m/s\), 3.6 \(m/s\), 5.3 \(m/s\), and 7.6 \(m/s\) – so with these numbers we would definitely not make categories A – C for Lawson and might even fail D as the threshold for that is 2%.
References
Last updated: July 29th, 2025
We appreciate and value your feedback.
Sign up for SimScale
and start simulating now