In fluid system design, managing pressure loss, or “head loss,” is essential for maintaining efficiency and functionality. Head loss refers to the reduction in pressure as fluids move through pipes and ducts, and it comes in two forms: major and minor head losses. Major head loss accounts for the pressure drop due to friction along straight sections of piping, while minor head losses arise from components like valves, fittings, and bends. Both types can significantly impact system performance, but accurately calculating major head loss is especially critical for fluid engineers, as it directly affects energy use, operational cost, and system reliability.
Using the Darcy-Weisbach equation, engineers can estimate major head loss based on pipe and fluid characteristics, but real-world conditions often complicate these calculations. Advanced simulation tools like SimScale provide a way to model head loss accurately, enabling engineers to visualize frictional impacts and optimize designs before implementation. In this article, we’ll explore the steps for calculating major head loss and show how simulation can play a vital role in creating efficient, reliable fluid systems.
Calculating Major Head Loss with the Darcy-Weisbach Equation
For engineers in fluid systems, the Darcy-Weisbach equation is essential for calculating major head loss. Named after hydraulic engineers Henry Darcy and Julius Weisbach, this equation reveals how fluid properties, pipe dimensions, and flow characteristics contribute to head loss, enabling engineers to design systems for optimal efficiency. It is expressed as follows:
$$ h_f = f \times \frac{L}{D} \times \frac{v^2}{2g} $$
Where:
- \(h_f\) = head loss due to friction (m or ft)
- \(f\) = Darcy friction factor (dimensionless)
- \(L\) = length of the pipe (m or ft)
- \(D\) = diameter of the pipe (m or ft)
- \(v\) = fluid velocity (m/s or ft/s)
- \(g\) = gravitational acceleration, typically 9.81 m/s2
The Darcy-Weisbach equation expresses head loss as a function of pipe characteristics, fluid velocity, and the friction factor. The friction factor depends on the flow regime, which is determined by the Reynolds number. For laminar flow, \(f\) can be calculated directly, but for turbulent flow, it varies with Reynolds number and pipe roughness. Here, engineers often use the Moody chart, a graphical representation of friction factors across various Reynolds numbers and relative roughness values. By locating the appropriate Reynolds number and roughness on the chart, engineers can quickly identify the friction factor, making the calculation process easier and more accurate.
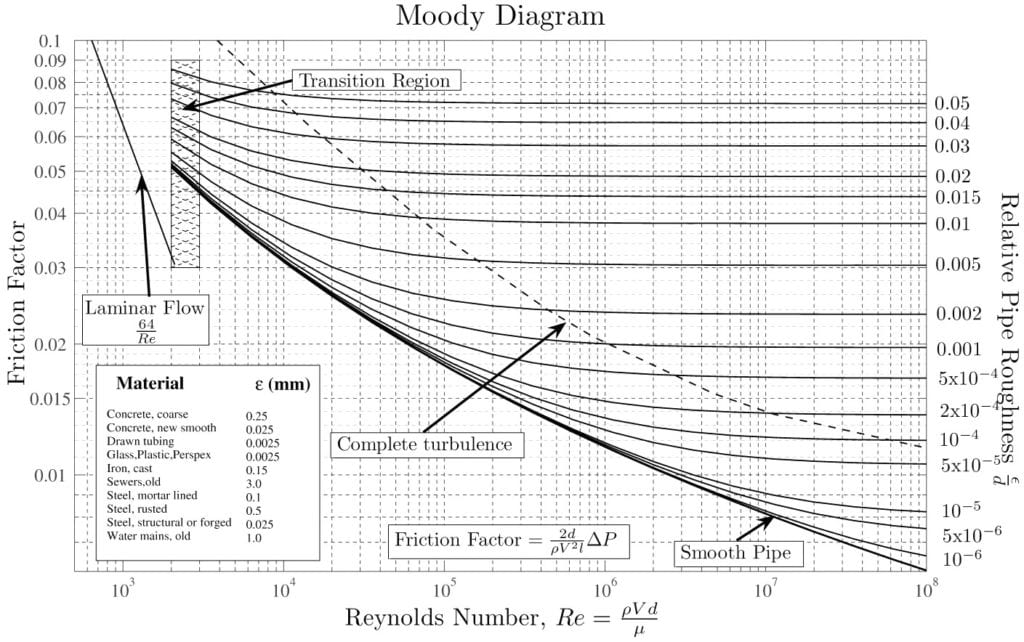
By accurately applying the Darcy-Weisbach equation and using tools like the Moody chart, engineers can anticipate frictional losses and design systems that perform reliably with minimal energy loss. Simulation tools like SimScale further support this process by simulating fluid behavior and validating head loss calculations, enhancing both speed and design precision.
Step-by-Step Guide to Calculating Major Head Loss
Calculating major head loss involves a few key steps, starting with identifying the flow regime, determining the appropriate friction factor, and then applying the Darcy-Weisbach equation. Let’s walk through each step.
1. Determine the Flow Regime
Start by calculating the Reynolds number \(Re\), a dimensionless number that classifies the flow as laminar or turbulent, which is crucial for selecting the correct friction factor. Use the formula:
$$ Re = \frac{v \times D}{\nu} $$
Where \(\nu\) is the kinematic viscosity of the fluid.
- If \(Re<2000\), the flow is laminar.
- If \(Re>4000\), it’s turbulent.
- Flows with \(Re\) between 2000 and 4000 are in the transitional range, and special considerations may be needed:
- Transitional flow (\(2000 < Re < 4000\)) is unpredictable and can shift between laminar and turbulent characteristics. For such cases:
- Stability Checks: Small changes in conditions may cause the flow to shift, so additional testing or simulation can help determine if it behaves more like a laminar or turbulent flow.
- Conservative Estimates: Using a friction factor closer to turbulent values can provide a safety margin in systems where precise control over pressure is critical.
- Use of CFD Software: Tools like SimScale CFD can help model transitional flows more accurately, offering insights beyond standard equations.
- Iterative Approach: Engineers may test both laminar and turbulent friction factors to gauge, which provides a more realistic estimate, adjusting the design as needed based on these calculations.
- Transitional flow (\(2000 < Re < 4000\)) is unpredictable and can shift between laminar and turbulent characteristics. For such cases:
2. Calculate the Friction Factor \(f\)
For Laminar Flow: The friction factor is simple to calculate using the formula:
$$f = \frac{64}{Re} $$
For Turbulent Flow: The friction factor depends on both the Reynolds number and the pipe’s relative roughness. The Colebrook-White equation is commonly used to calculate the friction factor for turbulent flow, though it requires an iterative approach:
$$ \frac{1}{\sqrt{f}} = -2 \log \left( \frac{\epsilon}{3.7D} + \frac{2.51}{Re \sqrt{f}} \right) $$
Here, \(\epsilon\) is the roughness height of the pipe material. Alternatively, a Moody chart can be used to find \(f\) based on \(Re\) and \(\epsilon/D\), saving time for engineers by avoiding the iterative calculation.
3. Substitute Values into the Darcy-Weisbach Equation
With the friction factor \(f\), pipe length \(L\), diameter \(D\), and fluid velocity \(v\) determined, substitute these into the Darcy-Weisbach equation to calculate head loss:
$$ h_f = f \times \frac{L}{D} \times \frac{v^2}{2g} $$
This provides the major head loss in meters or feet, depending on the units used, giving a tangible measure of the energy loss in the system.
4. Adjust for Unit Consistency
Ensure all units are consistent throughout the calculation to avoid errors. For example, if velocity is in meters per second and pipe diameter is in meters, gravitational acceleration should be in m/s².
Unit consistency is essential for accuracy, as mismatched units can lead to incorrect head loss values.
Example: Major Head Loss Calculation
An engineering team is designing a water distribution system for a small residential area. The system needs to supply water at a consistent pressure to all homes, so calculating the head loss in the main supply pipe is essential to ensure adequate pressure reaches each endpoint. The team has the following parameters for the pipe:
- Pipe length \(L=100 \, m\)
- Pipe diameter \(D=0.3 \, m\)
- Water velocity \(v=1.5 \, m/s\)
- Pipe material roughness \(\epsilon = 0.00015 \, m\) (for steel pipe)
- Water’s kinematic viscosity \(\nu = 1 \times 10^{-6} \, m^2/s\)
The goal is to determine the major head loss in the pipe section so they can ensure the system is designed with the right specifications.
Solution
1. Calculate the Reynolds Number:
Using the given values, we calculate the Reynolds number to determine the flow regime:
$$ Re = \frac{v \times D}{\nu} = \frac{1.5 \times 0.3}{1 \times 10^{-6}} = 450,000 $$
Since \(Re > 4000\), the flow is turbulent.
2. Determine the Friction Factor \(f\):
For turbulent flow, the friction factor depends on both Reynolds number and pipe roughness. Using the Colebrook-White equation or a Moody chart for turbulent flow, we find that: \(f \approx 0.02\)
3. Calculate the Major Head Loss:
Substitute the values into the Darcy-Weisbach equation to find the head loss:
$$ h_f = f \times \frac{L}{D} \times \frac{v^2}{2g} = 0.02 \times \frac{100}{0.3} \times \frac{1.5^2}{2 \times 9.81} = 5.1 \, m $$
The major head loss in this pipe section is, therefore, \(h_f = 5.1 \, m\).
The calculated head loss of 5.1 meters indicates the pressure drop due to friction over the 100-meter pipe length. This information helps the engineering team evaluate whether they need to adjust the pipe diameter, length, or pumping power to maintain adequate pressure in the distribution system.
For another example using SimScale, check out our validation case of a turbulent pipe flow.
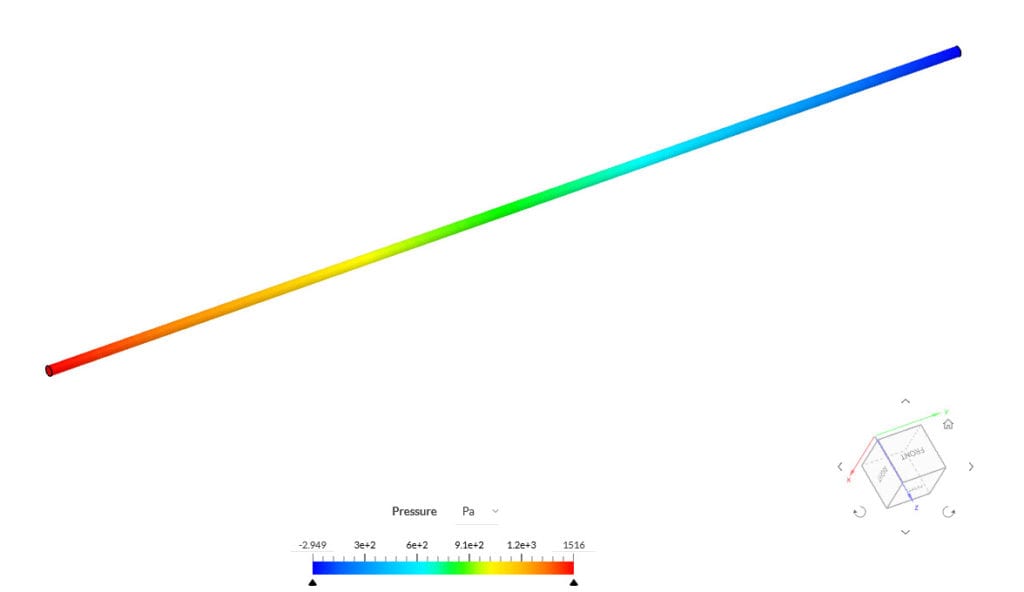
Factors Affecting Major Head Loss
As seen in the Darcy-Weisbach equation above, major head loss in a fluid system depends on a few critical factors: pipe diameter, length, fluid velocity, pipe roughness, and fluid viscosity. Each of these factors plays a vital role in determining the pressure drop due to friction along the length of a pipe, impacting the system’s efficiency, energy use, and maintenance costs.
Pipe Diameter
- Impact: Smaller pipe diameters increase head loss because friction becomes more significant relative to the flow area. In systems with high flow rates, narrow pipes lead to substantial pressure drops, which can reduce efficiency and require larger pumps to maintain desired pressures.
- Engineering Consideration: Engineers often balance pipe diameter with other design factors, such as material costs and space limitations. For critical systems, larger diameters may be selected to minimize head loss and reduce the load on pumps, improving long-term energy efficiency.
Pipe Length
- Impact: The longer the pipe, the greater the cumulative frictional losses, leading to a higher head loss. For systems covering large distances, such as municipal water networks, pipe length can significantly affect energy requirements.
- Engineering Consideration: In large facilities or expansive fluid networks, reducing unnecessary pipe length or adding intermediate pump stations can help mitigate head loss, maintain efficient flow, and reduce energy costs.
Fluid Velocity
- Impact: Higher fluid velocities increase head loss because frictional forces grow with the square of the velocity. While high velocities can improve flow rates, they also demand more energy to overcome increased friction, potentially leading to higher operational costs.
- Engineering Consideration: Engineers must carefully set flow velocity limits based on system requirements. In high-demand systems, velocity is optimized to balance efficiency with cost, as excessively high velocities can lead to rapid wear on pipes and fittings.
Pipe Roughness
- Impact: The roughness of the pipe material directly affects the friction factor in turbulent flow, with rougher surfaces (e.g., cast iron) creating more friction and increasing head loss. Conversely, smoother materials (e.g., PVC or stainless steel) reduce friction and are often used in systems requiring minimal head loss.
- Engineering Consideration: Engineers choose pipe materials based on both cost and performance. For systems where head loss is critical—such as high-precision HVAC or water distribution networks—smoother materials are preferred to keep energy usage low. Additionally, regular maintenance is essential to prevent surface degradation, which can increase roughness over time.
Fluid Viscosity
- Impact: Although viscosity does not change often in water systems, it is crucial in systems with oils, chemicals, or other viscous fluids. Higher viscosity increases resistance, which leads to greater head loss.
- Engineering Consideration: For fluid systems handling viscous substances, engineers may choose larger pipe diameters or lower flow rates to offset the increased head loss. Understanding the fluid’s viscosity at operating temperatures is also essential, as temperature changes can significantly alter viscosity and, consequently, head loss.
Practical Implications: These factors directly impact system design and operating costs. By analyzing how diameter, length, velocity, roughness, and viscosity influence head loss, engineers can make informed design choices that improve system efficiency, reduce energy consumption, and ensure reliable operation over the system’s lifetime. Simulation tools like SimScale can assist in evaluating these factors, allowing engineers to model different design scenarios and optimize for minimal head loss before physical implementation.
Optimizing Major Head Loss Calculations with SimScale
While a traditional equation like Darcy-Weisbach offers theoretical estimates, real-world systems often introduce complexities that make accurate predictions challenging. Here, simulation tools like SimScale bring significant advantages, helping engineers visualize, refine, and optimize head loss calculations with greater precision and efficiency.
1. Visualize Flow and Pressure Distribution
SimScale enables engineers to simulate fluid flow across piping networks, generating detailed visuals of pressure and velocity profiles. These simulations highlight areas of high head loss, offering insights that support targeted design adjustments, such as resizing pipes or changing materials, to maintain optimal flow and reduce frictional losses.
2. Refine Friction Factor Calculations
Determining the friction factor can be complex, especially for turbulent or transitional flow. SimScale enables engineers to input parameters like pipe roughness, Reynolds number, and flow conditions, which allows the platform to simulate flow behavior with these factors inherently considered. This approach provides a comprehensive understanding of head loss without requiring separate manual friction factor calculations, enabling engineers to design systems more confidently under varied flow conditions.
3. Test Multiple Scenarios Simultaneously for Design Optimization
With SimScale’s cloud-native platform, engineers can conduct multiple simulations concurrently, evaluating different design scenarios side by side. This capability enables rapid iteration and comparison of designs with varying pipe diameters, lengths, or materials, helping identify the configurations that minimize head loss while meeting other performance and cost requirements.
4. Account for Temperature-Dependent Fluid Properties
SimScale supports simulations that account for temperature variations and their effect on fluid properties like viscosity. This is essential for systems where temperature changes influence fluid behavior, such as HVAC systems or industrial pipelines carrying oils or chemicals. With temperature-dependent modeling, engineers can ensure the system’s performance remains consistent under varying operational conditions.
5. Minimize the Risk of Design Errors and Rework
By modeling head loss early in the design phase, SimScale helps engineers detect potential inefficiencies before physical implementation. This proactive approach reduces the risk of underperforming systems, excessive energy use, and costly modifications, as engineers can rely on accurate simulations to guide the design process.
6. Scale Complex Systems with Confidence
For large-scale systems, such as sections of municipal water networks or extensive industrial pipelines, calculating head loss across multiple pipe segments can be challenging. SimScale enables extensive system simulations, giving engineers a clear view of head loss distribution across key areas of the network. This approach ensures that critical components are sized appropriately, reducing strain on pumps and improving overall system performance.
Conclusion
Effective management of major head loss is essential for the efficiency and longevity of fluid systems. By leveraging SimScale’s advanced simulation tools, engineers can go beyond theoretical calculations to gain deeper insights into flow dynamics, identify potential inefficiencies, and fine-tune designs to meet real-world demands. With its cloud-based platform, SimScale enables rapid iteration and scalability, making it a valuable asset for engineering teams aiming to optimize system performance and reduce operational costs in complex, large-scale networks.
