One of the key factors in a numerical simulation is determining the appropriate mathematical model which describes the physics of the problem. Almost every engineering problem comprises interactions between matter: water, air, oil, etc. For this reason, the analyst should carefully specify the problem, taking these factors into consideration. In order to understand multiphase flow properly, it is necessary to first explain the basics of the physical phenomenon.
Matter: Matter is defined as a physical structure that has mass and volume in space. It comprises all forms of physical elements that exist in the form of atoms. Uranium, water, salt, and even a piece of wood, are all expressed as matter.
Phase: It is a distinctive form of matter with three types:
- Solid: Shape and volume are definite
- Liquid: Volume is definite, yet the shape belongs to the container
- Gas: Shape and volume belong to the entire structure of the container
Interface: In a system with different phases, a narrow and distinct region, known as the ‘phase interface’, emerges. The phases on either side of the interface have different chemical and physical properties, and mathematical expressions are required to model the transport of mass, momentum, and energy across the interface.
Some examples of multiphase flows include a mixture of liquid mercury and liquid water and phase-changing processes like the transition of ice into liquid water. The expression of multiphase fluid flow might be indicated as “number of phases” + “flow” in accordance with the total number of phases. For instance, the mixture of liquid water and liquid oil can be classed as a two-phase flow or a multiphase flow. On the upshot, multiphase flow is the interaction of more than one matter or phase of matter that exists simultaneously. Transportation of mass, momentum, and energy among phases—based on conservation laws—is examined through the simulation.
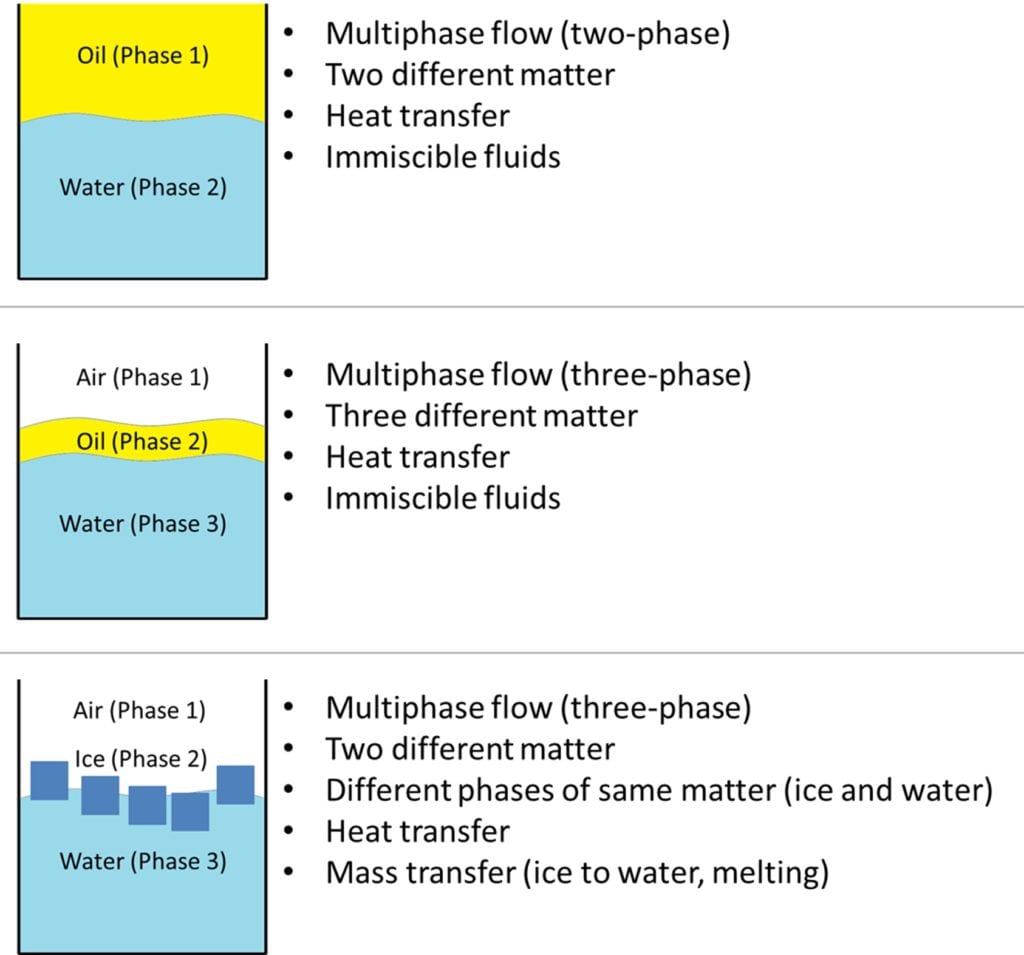
Multiphase Flow Models
For the purpose of carrying out a reliable numerical simulation, the mathematical model which describes the physics should be scrutinized. For instance, transition among phases such as condensation, requires an appropriate mathematical model, correlation, or theory which defines the condensation process as accurately as possible.
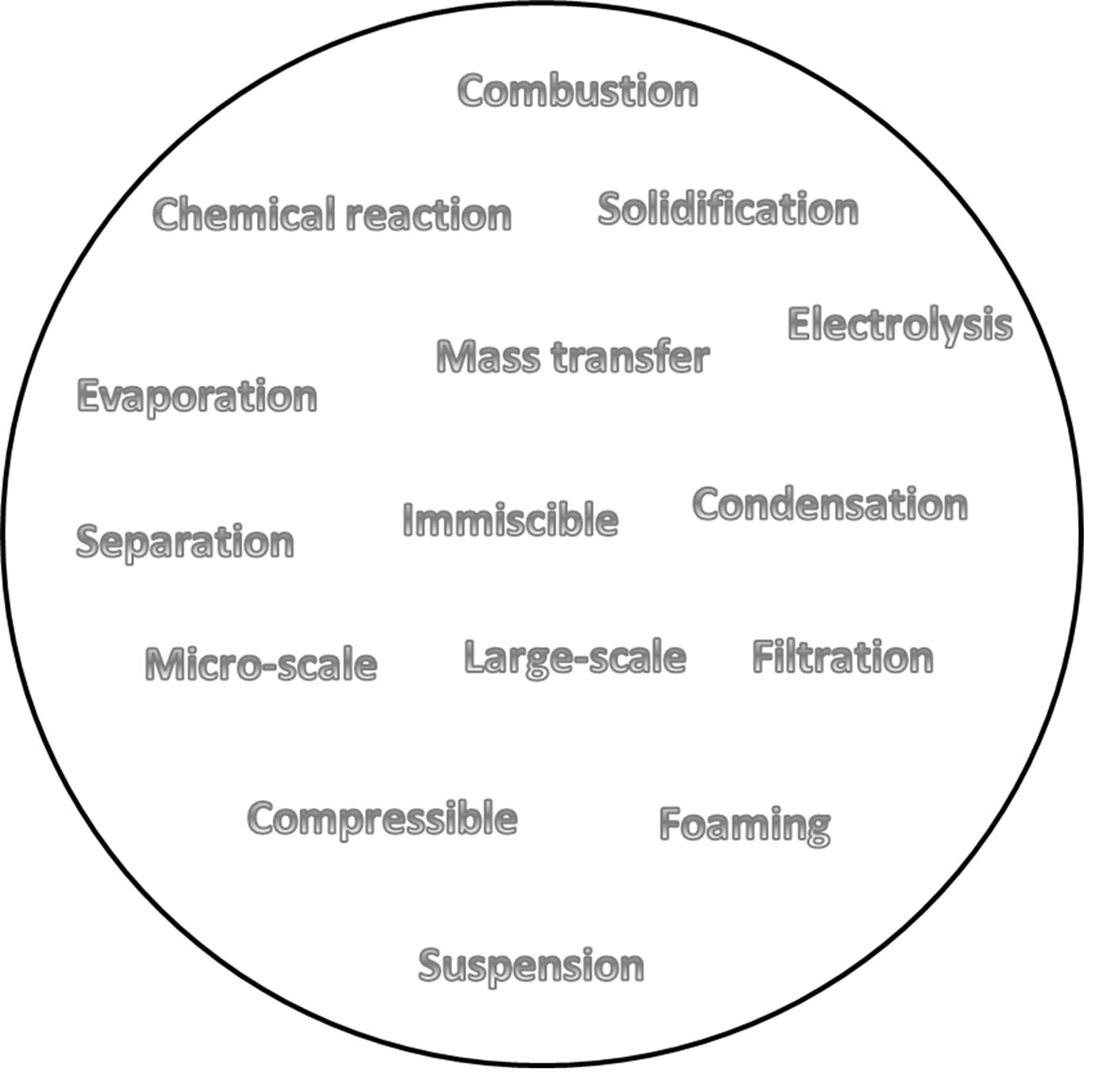
Generally, the modeling process of multiphase flow includes three main stages, which are the description of the physical process, the specification of the flow, and the determination of the suitable mathematical model.
SimScale Launches New Multiphase Flow Capabilities
Description of the Physical Process
In the case that fluid flow comprises more than one phase, the physical model should be defined properly to describe the governing process so as to herald fluid flow and even mathematical model. Some of the processes and models might be specified concerning multiphase flow, as illustrated in Figure 2.
Specification of the Fluid Flow Regime
There are various types of multiphase fluid flow in the literature that diversify in accordance with the physical process and properties of the problem, and these can be classified into three main fields:
Separated Phases: More than one immiscible fluid in continuous phases and separated by interface [1].
Mixed Phases: Presence of both separated and dispersed phases [2].
Dispersed Phases: Finite numbers of phases spread through the volume of continuous phases such as droplets, drops, particles, or bubbles [1].
Various types of fluid flow can be classified, as shown in Figure 3:
![Multiphase fluid flows according to types of phases [2]](https://www.simscale.com/wp-content/uploads/2017/12/flow.jpg)
The Mathematical Model
The discrimination of phases in the numerical simulation relies on the rate of volume or mass. To determine an appropriate mathematical model for fluid flow, factors such as physical process and flow regime have to be described in advance. Several mathematical models have been developed in order to properly simulate fluid flow. The investigation of multiphase flow still has several hindrances due to complexities related to the mathematical models. However, the Navier-Stokes equations might be broadly used to examine multiphase flows, and the capability of hardware in conducting numerical studies, which are reliant on Navier-Stokes equations, is still far from an affirmative solution.
Over and above that, a challenging model—such as those related to turbulence, chemical reaction, or mass transfer—carries the problem to a further level of complexity. For this reason, generating both realistic and simpler models is the key factor for multiphase fluid flow simulations [1]. The most commonly used mathematical approaches—such as empirical correlations—might be conducted as follows [3]:
- Volume of Fluid (VOF): Separated flows, free surface flows
- Lagrangian Multiphase (LMP): Droplet flows, track individual point particles, particles do not interact
- Discrete Element Method (DEM): Particle flows, solve the trajectories of individual objects and their collisions, inside a continuous phase
- Eulerian Multiphase (EMO): Dispersed flow, particle flows, bubbly flows, boiling heat and mass transfers, interphase mass transfer
- Eulerian/Lagrangian Dispersed Phase Model (DPM): Particle-wall interaction is always considered, particle-particle is usually not
- Eulerian-Eulerian Model (EEM): Particle-wall interaction is considered, particle-particle is usually not
- Eulerian-Granular Model (EGM): Both particle-wall and particle-particle interaction are considered
Apart from the models above, further miscellaneous models can be found in the literature according to the type of fluid flow.
Application of Multiphase Flow
Many engineering problems depend on the numerical examination of fluid flow, which typically comprises more than one phase. Automotive, power generation, chemical industry, food industry, environment, and even medicine are some sectors that have been using numerical tools to predict the outcomes in advance. To learn more about multiphase simulation within SimScale, check out the latest features in this on-demand webinar.

References
- C. E. Brennen, 2005, Fundamentals of Multiphase Flows, Cambridge University Press, ISBN: 0521 848040
- Multiphase systems and phase changes: https://www.thermalfluidscentral.org/e-resources/download.php?id=72
- Applied Computational Fluid Dynamics, André Bakker


